- At the design stage, we focus on specific facets of the systems.
- At run time, these facets need to fit together correctly.
- Composing systems is rarely as simple as composing functions.
- The task becomes harder when many domain experts are involved.
Principles
Our systems development is guided by mathematically precise design principles.
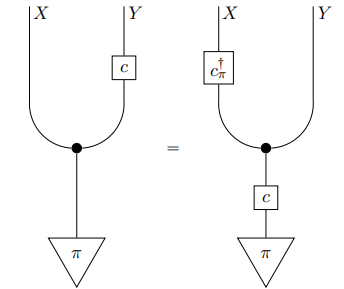
To build modular systems, we define components as morphisms, i.e. abstract maps with generalized notions of composability. These morphisms compose only when their inputs and outputs have matching types, giving us highly reliable systems.
The facets of a system are like the layers of a map. The layers are designed by domain experts who may use different ontologies. To glue the layers into a map, we relate the ontologies via morphisms between layers before constructing the composite.
Describing a complex system with a web of morphisms is akin to defining a deep neural net by its computational graph. Using functors, we assign meanings to the morphisms in some compute framework, giving us efficient executable code.
Highlights
Many of our projects fall under the AlgebraicJulia project, a collaborative open-source framework for scientific modeling, data organization, project management, and decision-making. Topos is a key contributor to AlgebraicJulia, alongside our collaborators from:
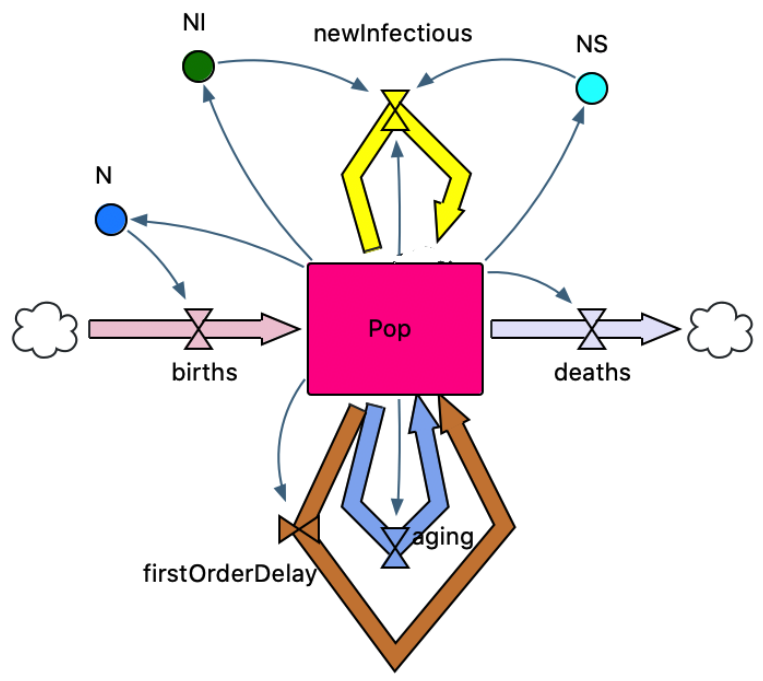
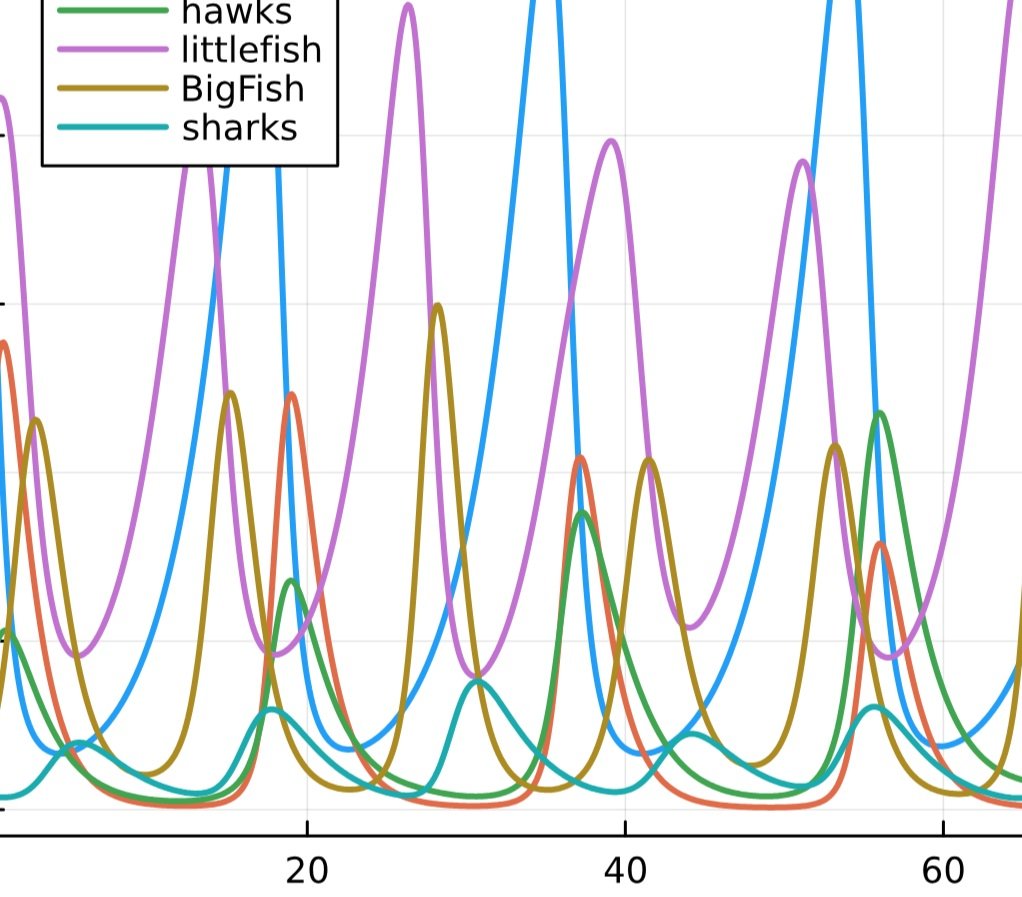
Collaborative pandemic modelling
Epidemiologists use stock-flow diagrams to describe disease dynamics. Together with the University of Saskatchewan and UC Riverside, we built the StockFlow.jl library and the ModelCollab web interface for designing and composing stock-flow diagrams using decorated cospans, as explained on our blog.
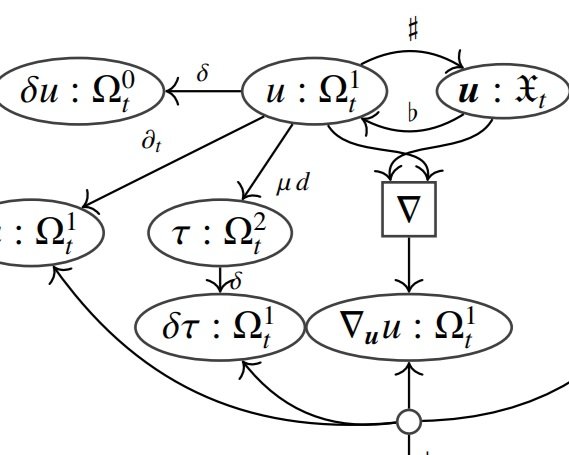
Diagrammatic differential equations
In our research paper with collaborators, we develop a diagrammatic framework for presenting and solving differential equations in physics, as explained on our blog. The Decapodes.jl library adapts these methods to engineering, merging models across electrical, mechanical, and aeronautical systems.
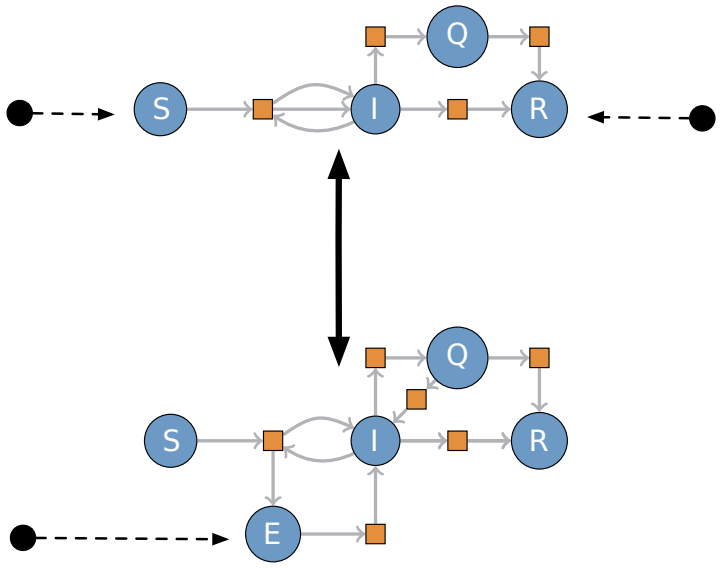
Efficient graph rewriting
We demonstrate how category theory provides specifications that can be implemented efficiently via imperative algorithms and apply this to the field of graph rewriting. Our AlgebraicRewriting.jl library makes it easy to quickly write correct and performant code.
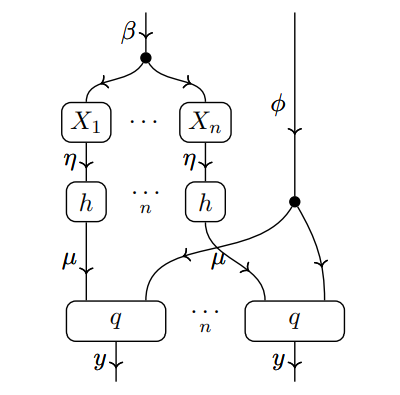
Generalised statistical theories
In this AFOSR project, we draw a precise analogy between models in statistics and logic using categorical logic. Statistical theories, being algebraic structures, are amenable to machine representation and are equipped with formal morphisms between different statistical methods.

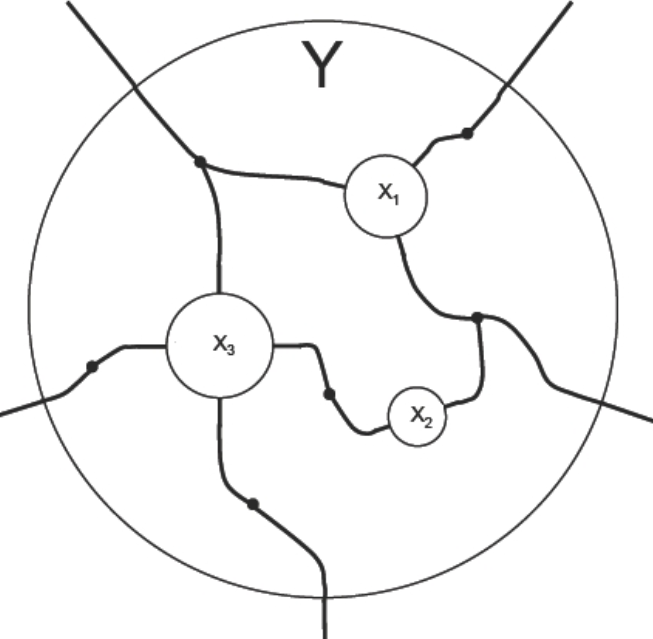
Interactive string diagrams
Semagrams.jl is a tool for interacting with semantic diagrams. Semantic diagrams are graphical representations of data that have teeth, i.e. where there is a formal and machine-readable correspondence between the graphical display and its semantic meaning.
Operadic systems engineering
With the US National Institute of Standards and Technologies (NIST) and Carnegie Mellon University, we are adapting AlgebraicJulia for project management in systems engineering, to show its effectiveness for shared decision-making across multiple complex systems.
No matching items
Select publications
Baez, John, Xiaoyan Li, Sophie Libkind, Nathaniel Osgood, and Evan Patterson. 2022.
“Compositional Modeling with Stock and Flow Diagrams.” In
5th International Conference on Applied Category Theory.
https://msp.cis.strath.ac.uk/act2022/papers/ACT2022_paper_8631.pdf.
Brown, Kristopher, Evan Patterson, Tyler Hanks, and James Fairbanks. 2023.
“Computational Category-Theoretic Rewriting.” Journal of Logical and Algebraic Methods in Programming 134.
https://doi.org/10.1016/j.jlamp.2023.100888.
Libkind, Sophie, Andrew Baas, Evan Patterson, and James Fairbanks. 2021.
“Operadic Modeling of Dynamical Systems: Mathematics and Computation.” In
4th International Conference on Applied Category Theory.
https://www.cl.cam.ac.uk/events/act2021/papers/ACT_2021_paper_53.pdf.
Patterson, Evan, Andrew Baas, Timothy Hosgood, and James Fairbanks. 2022.
“A Diagrammatic View of Differential Equations in Physics.” Mathematics in Engineering 5.
https://doi.org/10.3934/mine.2023036.
St. Clere Smithe, Toby. 2022.
“Compositional Active Inference II: Polynomial Dynamics. Approximate Inference Doctrines.” https://arxiv.org/abs/2208.12173.
“The AlgebraicJulia Project.” 2023. 2023.
https://www.algebraicjulia.org/.