Compositional Thermostatics
In this post, we explore the compositionality of thermodynamic systems at equilibrium (thermostatic systems). The main body of this uses no category theory, and reviews the physics of thermostatic systems in a formalism that puts entropy first. Then there is a brief teaser at the end showing how this entropy-first approach can be treated categorically.
1 Introduction
Thermostatics is the study of thermodynamic systems at equilibrium. Typically people call this subject “equilibrium thermodynamics”, but we prefer “thermostatics” because it is in analogy with other physical disciplines such as “electrostatics”.
Traditionally, thermodynamics is a subject impenetrable to any with a good sense of mathematical rigor. In the appropriately named “The Tragicomical History of Thermodynamics”, Clifford Truesdell describes the state of thermodynamics in 1980 as “a dismal swamp of obscurity”, and goes on to proclaim that there is “something rotten in the [thermodynamic] state of the Low Countries”. (cited in [1]). Unlike other fields of physics, like classical mechanics, relativity, quantum mechanics, or even statistical mechanics, thermodynamics has so far (to my knowledge) eluded a well-accepted formal mathematical framework, and this is in spite of its incredible importance to chemistry, biology and engineering.
In this blog post, I aim to bring the mathematical reader out of this swamp, and show that there is a formulation of thermostatics that is both mathematically precise and simple. To this end, I will start with an axiomatic framework for thermostatics, slightly more rigorous than the axiomatic framework one often sees in the beginning of a physics book, but still not perfectly precise. This axiomatic framework will be accompanied by examples and physical reasoning as motivating material. For the sake of pedagogy, this will be less general than possible, and also somewhat flawed.
I will then reformulate the axiomatic framework in categorical terms, which leads to more rigorous and general setting. Finally, I will conclude with a teaser of something surprising that can be done within this categorical framework. This blog post is a preview of some content that I will be releasing a paper on with John Baez and some other collaborators, and what I am teasing will be fleshed out in more detail there.
2 An Axiomatic Framework for Thermostatics
Before we begin, a brief note on the use of axioms rather than definitions, which are more typical in a mathematical setting. This section is intended to give a physical intuition for why my mathematical definitions in the next section are natural. Therefore, the real content of these axioms is the assertion that they correspond to physical reality. We have some intuition in our heads already for thermostatic equilibrium, where we expect that things touching each other should have the same temperature, and we expect gas to be distributed uniformly in a container. Rather than just stating definitions, these axioms are claiming that our experience of the world is in accordance to a certain formalism.
Inspiration for this axiomatic framework is due to the opening chapter of [2].
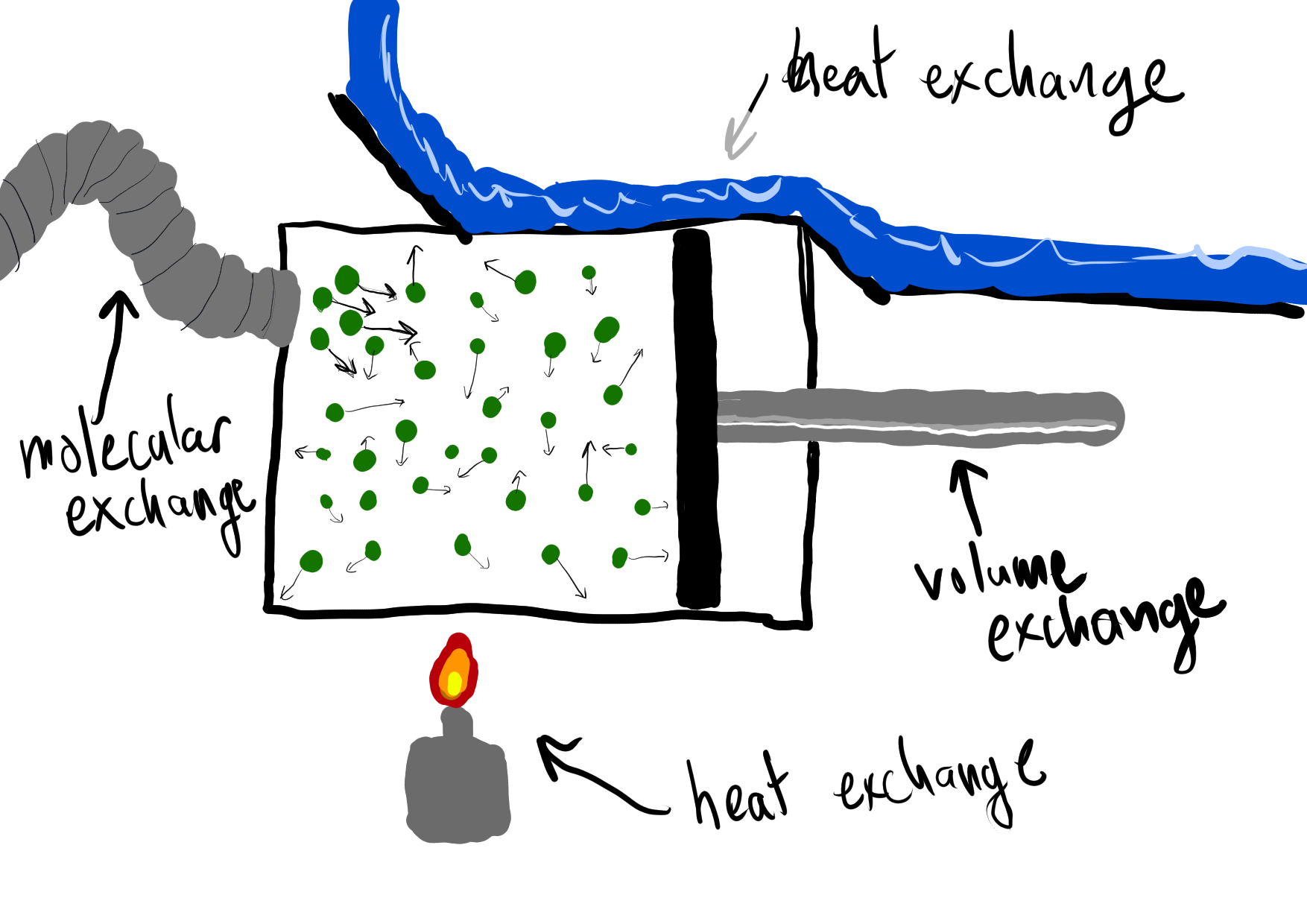
When we are talking about systems that are given by subscripts on \Sigma, i.e. \Sigma_{1}, \Sigma_{2}, we will typically refer to the state space and entropy function by \mathbb{X}^{1}, S^{1}.
The independent sum of two thermostatic systems corresponds physically to putting the two systems together and not letting them interact.
This is not a particularly exciting way of composing systems. Intuitively, if one has two rocks that are touching, the state where one is very hot and the other is very cold is not an equilibrium state, and we want to capture this. To capture this formally, let’s talk about what equilibrium means in this context.
In physics, there is a “maximum entropy” principle, which says that equilibrium happens at the state of highest entropy. However, this must be modified slightly in order to work, because we need to be careful about which states we are considering. That is, we want to say that equilibrium happens at the state of highest entropy with respect to contraints put on the system.
As an example, consider the following interactive applet, which attempts to layout a graph at a local maximum of some “goodness of layout” function, left unspecified. The red nodes are unconstrained, and when you click and drag on one, it becomes blue and stays in place. Clicking on it again returns it to an unconstrained red state. The applet attempts to find the best layout with respect to the constraints put on it by the blue nodes.
We describe this by calling a position of all the nodes an “endostate” (or internal state), and a position of the blue nodes an “exostate” (or external state). The system attempts to find an equilibrium endostate compatible with an exostate. We formalize this intuition with an axiom.
One justification for this axiom in terms of classical thermodynamics is that the second law says that entropy always increases. Therefore, a point of equilibrium for any constrained system must be a highest entropy state for that system subject to those constraints.
The problem with the classical second law, however, is that the second law refers to a dynamical system, whereas classical thermodynamics deals only with systems at equilibrium. No wonder thermodynamics was called a swamp!
Also, one should note that with our definition, S^{\mathbb{Y}}(Y) could be the supremum of an empty set, or an unbounded set. Moreover, there’s no guarantee that S^{\mathbb{Y}} is differentiable. In the categorical section, we address both of these problems; for now… just don’t choose bad R OK?
For our final axiom, we will first give some physical arguments for a couple of propositions. These arguments are typical of physics textbooks and are not rigorous, relying on our physical intuition for what “equilibrium” means. Their purpose is to motivate Axiom 4, by connecting it to our intuitions about the physical world.
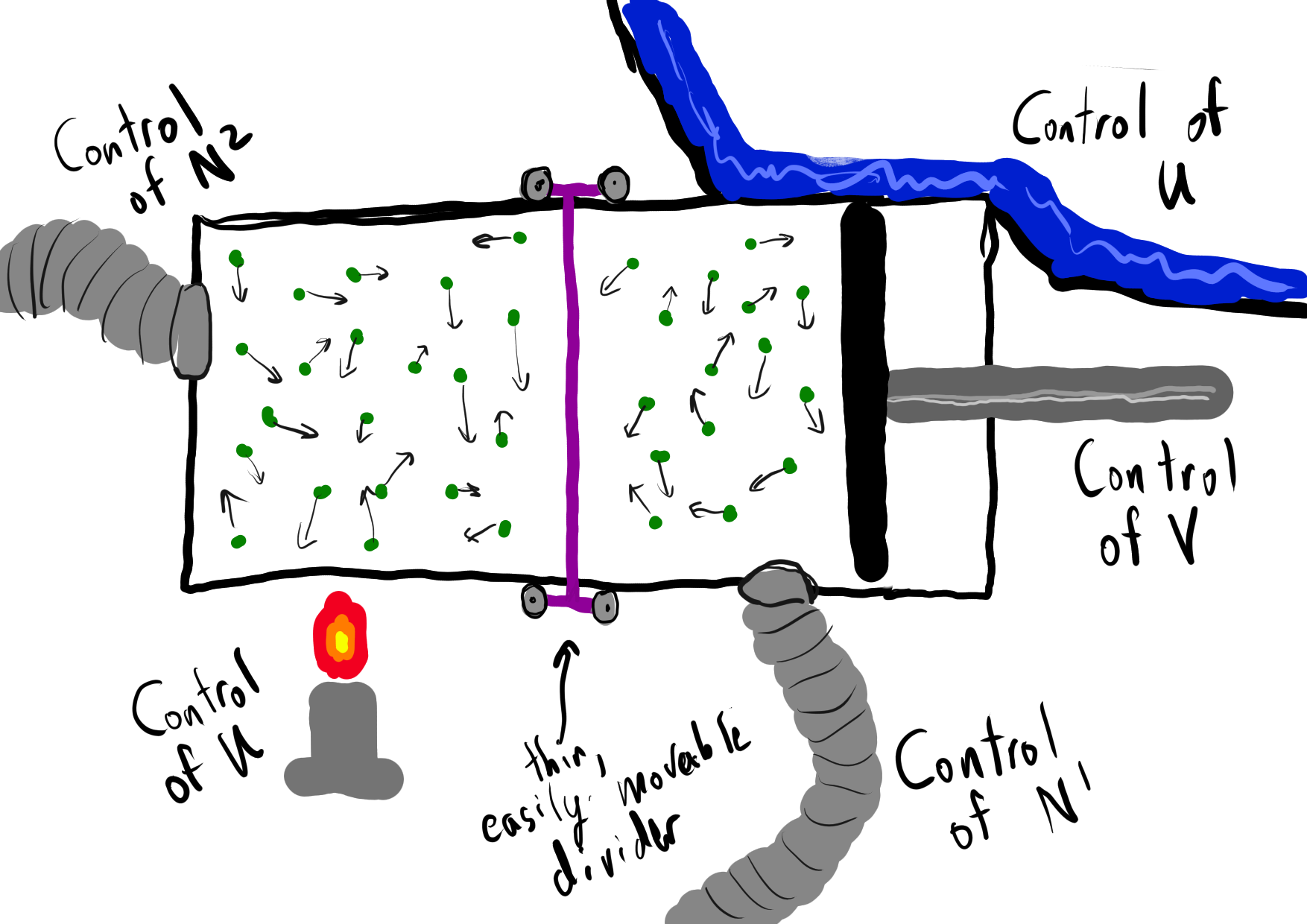
Proof. To show this, consider an ideal gas in a box split in half by an imaginary wall. The exostates that we will consider are the standard (U,V,N), and the endostates compatible with (U,V,N) are all (U^{1}, V^{1}, N^{1}), (U^{2}, V^{2}, N^{2}) such that
U^{1} + U^{2} = U N^{1} + N^{2} = N V^{1} = \frac{1}{2}V V^{2} = \frac{1}{2}V
Our physical intuition tells us that equilibrium happens when U^{1} = U^{2} = \frac{1}{2} U and N^{1} = N^{2} = \frac{1}{2} N. That is, this is the endostate that maximizes the entropy. Thus, by the definition of exostate entropy as the maximum over compatible endostate entropies.
S(U, V, N) = S(\frac{1}{2} U, \frac{1}{2} V, \frac{1}{2} N) + S(\frac{1}{2} U, \frac{1}{2} V, \frac{1}{2} N) = 2 S(\frac{1}{2} U, \frac{1}{2} V, \frac{1}{2} N)
and thus \frac{1}{2} S(U,V,N) = S(\frac{1}{2} U, \frac{1}{2} V, \frac{1}{2} N).
Splitting the box into n equal parts similarly shows that \frac{1}{n} S(U,V,N) = S(\frac{1}{n} U, \frac{1}{n} V, \frac{1}{n} N), and then some algebra shows that
S(\lambda U, \lambda V, \lambda N) = \lambda S(U,V,N)
for all positive, rational \lambda. Finally, invoking continuity shows it for all \lambda.
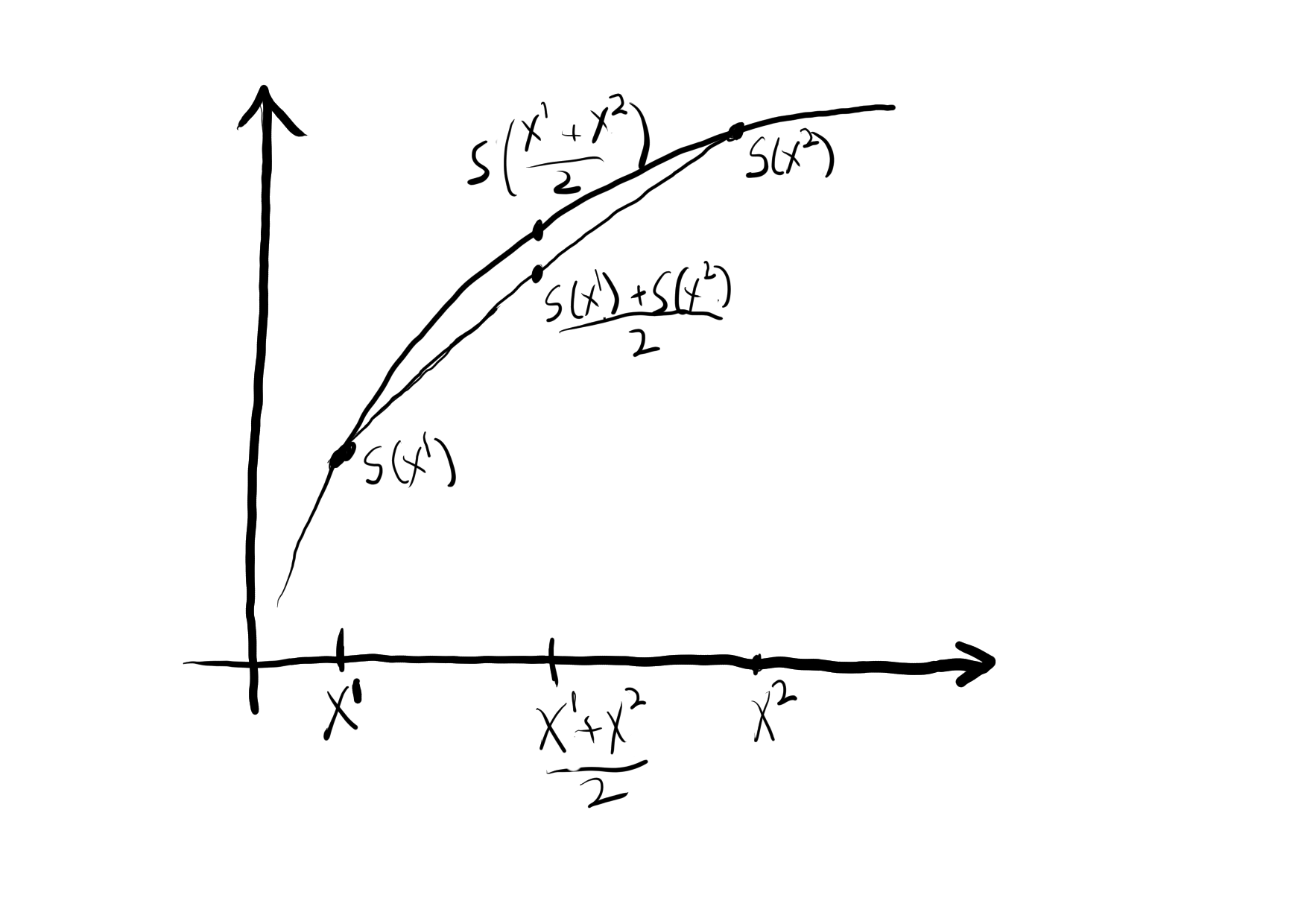
As a reminder what this means geometrically, here is a graph of a concave function.
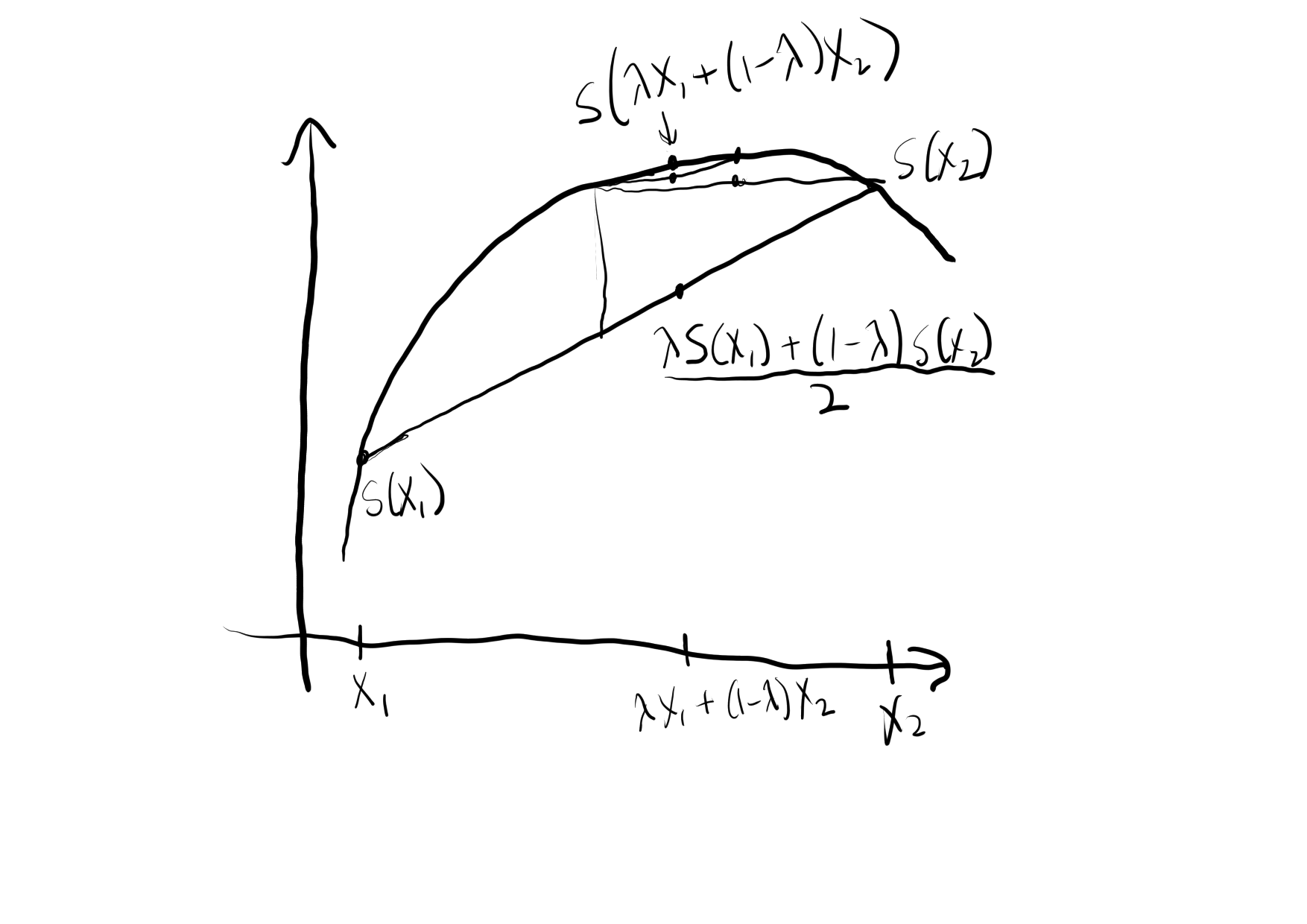
Proof. We first show this for \lambda = \frac{1}{2}.
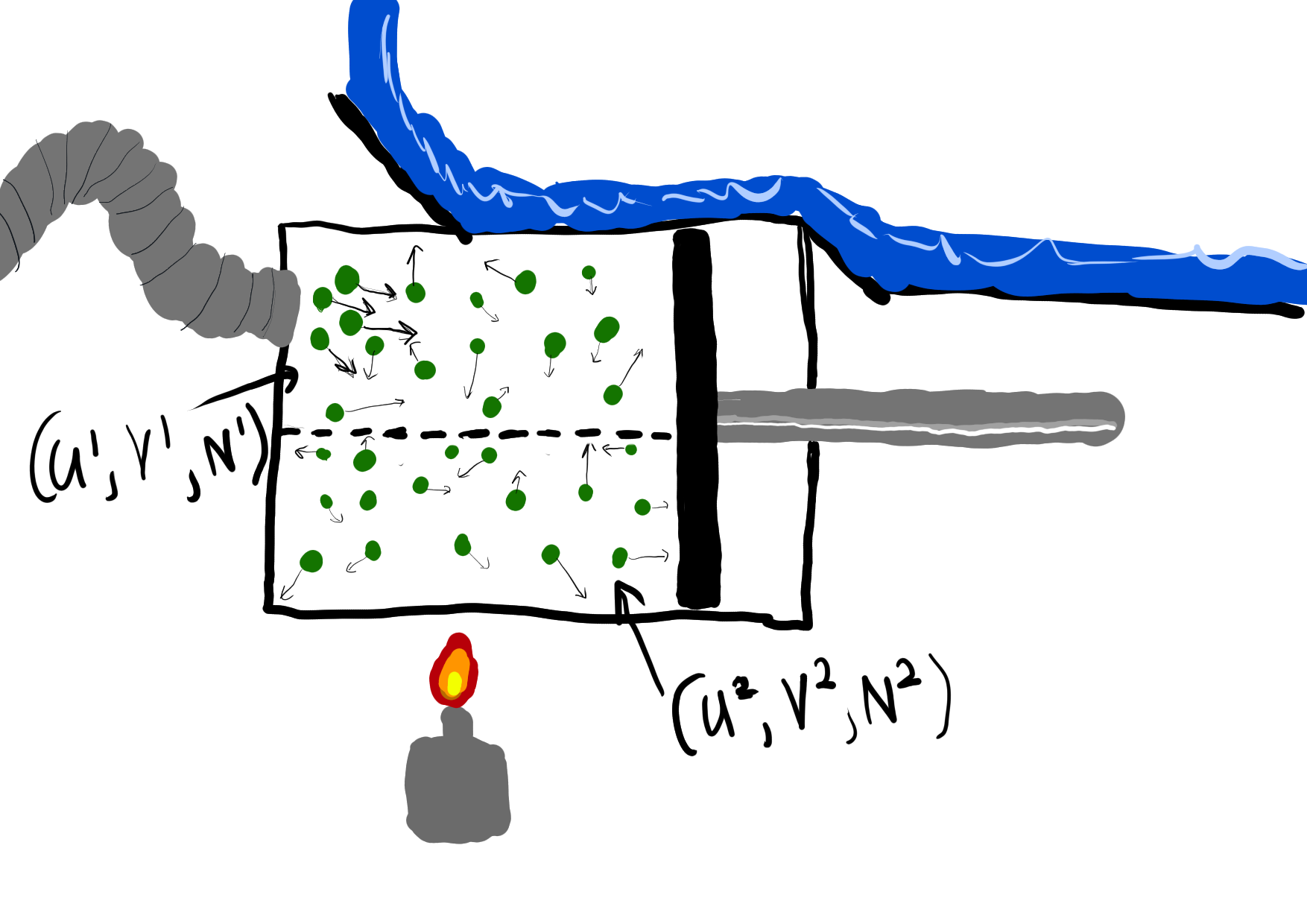
Again, consider the ideal gas with an imaginary divider, but this time suppose that the divider can move. Let (U^{1}, V^{1}, N^{1}) and (U^{2}, V^{2}, N^{2}) be two possible states of an ideal gas. Then fix an exostate of the “ideal gas with imaginary divider” system: U = U^{1} + U^{2}, V = V^{1} + V^{2}, N = N^{1} + N^{2}. An endostate that is clearly in thermal equilibrium with this exostate is
U^{1}_{\mathrm{eq}} = U^{2}_{\mathrm{eq}} = \frac{U^{1} + U^{2}}{2} V^{1}_{\mathrm{eq}} = V^{2}_{\mathrm{eq}} = \frac{V^{1} + V^{2}}{2} N^{1}_{\mathrm{eq}} = N^{2}_{\mathrm{eq}} = \frac{N^{1} + N^{2}}{2}
Therefore, by definition of thermal equilibrium,
S(U^{1}, V^{1}, N^{1}) + S(U^{2}, V^{2}, N^{2}) \leq 2 S(\frac{U^{1} + U^{2}}{2},\frac{V^{1} + V^{2}}{2},\frac{N^{1} + N^{2}}{2}) \frac{S(U^{1}, V^{1}, N^{1}) + S(U^{2}, V^{2}, N^{2})}{2} \leq S(\frac{U^{1} + U^{2}}{2},\frac{V^{1} + V^{2}}{2},\frac{N^{1} + N^{2}}{2})
This is what we wanted for \lambda = \frac{1}{2}. To show it for all \lambda, we sequentially subdivide as shown in the following picture. That we can do this is a standard fact for continuous concave function.
As I said before, these arguments are not really proofs, but rather appeals to our physical intuition about what “equilibrium” means. To bring this into mathematics, we take what we have just argued for as an axiom.
Entropy being concave also means that the partial derivative of entropy with respect to, for instance, energy, is always decreasing. This means that temperature increases as energy increases, which is physically true, so it’s a good thing that it’s true in our formulation.
But more fundamentally, entropy being concave means that “mixing” two states (via convex combination) always results in a greater than or equal entropy to the convex combination of the original entropies. Mixing raising entropy is arguably a fundamental property of anything that should be called entropy, just on the intuition that entropy measures how “mixed up” a state is.
Note that we do not include homogeneity of entropy as an axiom. We could do this in our current framework, because we have restricted state spaces to be \mathbb{R}^{n}_{>0}. This is because of the following thermostatic system, which violates Axiom 1.
One of the exciting features of the formulation of thermostatics that I will present in the next section is that it is flexible enough to capture the previous example, and talk about how it relates to models like the classical ideal gas given by (U,V,N) coordinates, which means that this formalism edges in on the territory of statistical mechanics.
3 The Categorical Perspective
The categorical perspective on thermostatics repackages the four axioms listed above into a more elegant and rigorous framework. The axioms don’t quite map cleanly onto the parts of the categorical perspective; they rather come together and then come apart in a different organization. However, one can certainly see how each axiom comes into the framework in its own way.
We start with the category \mathsf{ConvRel} which has
- as objects convex spaces (i.e., convex subsets of vector spaces)
- as morphisms convex relations. A convex relation between \mathbb{X} and \mathbb{Y} is simply a convex subset of \mathbb{X} \times \mathbb{Y}.
In the language of thermostatics, an object of \mathsf{ConvRel} is a state space, and a morphism R \subseteq \mathbb{X} \times \mathbb{Y} is a way of seeing \mathbb{X} as the endostates of a system, and \mathbb{X} as the exostates. R is the compatibility relation; (X,Y) \in R if X is compatible with Y.
We then make a functor \mathrm{Ent} \colon \mathsf{ConvRel} \to \mathsf{Set}, which sends a state space \mathbb{X} to \mathrm{Ent}(\mathbb{X}) = \{ S \colon \mathbb{X} \to \bar{\mathbb{R}} = \mathbb{R} \cup \{ -\infty, +\infty \} \mid S \text{ is concave}\}. That is, it sends a state space to the set of compatible entropy functions. Note that we have not required these entropy functions to be differentiable, but we have required them to be concave. Moreover, entropy can be positive or negative infinity; this is necessary because the supremum of an empty set is -\infty and the supremum of an unbounded set is +\infty.
On morphisms, we must take a convex relation R \subseteq \mathbb{X} \times \mathbb{Y} (which we view as an endostate/exostate compatibility relation) to a function \mathrm{Ent}(R) \colon \mathrm{Ent}(\mathbb{X}) \to \mathrm{Ent}(\mathbb{Y}). To define \mathrm{Ent}(R), we must take a entropy function on \mathbb{X} and produce an entropy function on \mathbb{Y}. Axiom 3 tells us exactly how to do this: given an entropy function S^{\mathbb{X}} \colon \mathbb{X} \to \bar{\mathbb{R}}, we produce an entropy function S^{\mathbb{Y}} \colon \mathbb{Y} \to \bar{\mathbb{R}} by
S^{\mathbb{Y}}(Y) = \sup_{(X,Y) \in R} S^{\mathbb{X}}(X)
In words, the entropy function on \mathbb{Y} sends an exostate to the maximum of entropies of compatible endostates. This new entropy function S^{\mathbb{Y}} is also concave because R is a convex relation (which is not trivial to show, but also not too hard).
So far, we have covered axioms 1, 3, and 4. The remaining axiom, axiom 2, allows us to take an entropy function on \mathbb{X}^1 and an entropy function on \mathbb{X}^2 and construct an entropy function on \mathbb{X}^{1} \times \mathbb{X}^{2}. This is simply expressed as a function in \mathsf{Set}
\kappa_{\mathbb{X}^{1},\mathbb{X}^{2}} \mathrm{Ent}(\mathbb{X}^{1}) \times \mathrm{Ent}(\mathbb{X}^{2}) \to \mathrm{Ent}(\mathbb{X}^{1} \times \mathbb{X}^{2})
which is natural in \mathbb{X}^{1} and \mathbb{X}^{2}. That is, \kappa is a natural transformation between two functors \mathsf{ConvRel} \times \mathsf{ConvRel} \to \mathsf{Set}, the first sending (\mathbb{X}^{1}, \mathbb{X}^{2}) to \mathrm{Ent}(\mathbb{X}^{1}) \times \mathrm{Ent}(\mathbb{X}^{2}), and the second sending (\mathbb{X}^{1}, \mathbb{X}^{2}) to \mathrm{Ent}(\mathbb{X}^{1} \times \mathbb{X}^{2}).
Categorically speaking, all of this structure has a name. (\mathrm{Ent}, \kappa) is known as a lax monoidal functor between the monoidal categories (\mathsf{ConvRel},\times) and (\mathsf{Set},\times).
So, in the grand tradition of category theorists boiling down something very complex into tightly wrapped package, we might say “thermostatics is just the study of a particular lax monoidal functor from (\mathsf{ConvRel}, \times) to (\mathsf{Set},\times)”. And there is a way of repacking this definition into yet another package, using operads and operad algebras, but we will not delve into this here.
The reader who wishes to get more of an intuition for this construction is encouraged to go back to the examples of ideal gases and lumps of metal in the previous section and reformulate them in a more categorical context.
The last example I will give of this formalism, which I mentioned at the end of the previous example, I will give briefly; and you must wait for a subsequent blog post or paper for it to be realized in full detail.
It was very surprising to me that this framework which I came up with to do macroscale thermostatics also seems to have inherent connections to statistical mechanics; it seems like I must be on to something.
Exactly what I am onto will have to wait until the future, however.
If you find this kind of thing interesting, please reach out to me, my email is “owen at topos dot institute”.