Playing with Shapes at Topos
This month sees a new person joining the team here at Topos: we’re thrilled to welcome Brandon Shapiro! He’s working with David Spivak on the theory and applications of polynomial functors. We asked him to write a short blog post introducing both himself and his mathematics.
I recently started working at Topos Institute! Here’s a bit about me and the things I work on…
I started doing math because it helped me see beautiful impossible shapes in my head. Eventually I realized math could help me see other things too, like how different mathematical structures are actually very similar, as are structures in the real world when viewed from a particular angle. I’m interested in many very different things, but I think the most clearly about shapes, so most of my mathematical work is about turning things into shapes so they make more sense to me. Category theory makes this kind of translation possible, and I hope to make its services more widely available so lots of people can think about things in the way that is easiest for them and still communicate with others who think entirely differently.
As a PhD student at Cornell, I studied homotopy theory, algebraic K-theory, and lots of categories. In 2019 I started learning about applied category theory with Carmen Constantin, Tobias Fritz, Martin Lundfall, and Paolo Perrone, to better understand how algebraic expressions like 1+2+3 are evaluated in steps: the eventual result is always 6, but it could pass through 1+5 or 3+3 along the way. Each step can be treated as an arrow from one expression to another, and deeply nested expressions like ((1)+(2+3))+((4)) can be treated like higher dimensional cells in a space with interesting computational meaning. I also worked on algebraic K-theory projects with Jonathan Campbell, Maru Sarazola, and Inna Zakharevich (my advisor), where we used composable squares in a double category to analyze how things (like sets or modules or spaces) can be broken up into smaller pieces and put back together. I used to be intimidated by homological algebra, but now I can think of it entirely in terms of moving around squares and arrows.
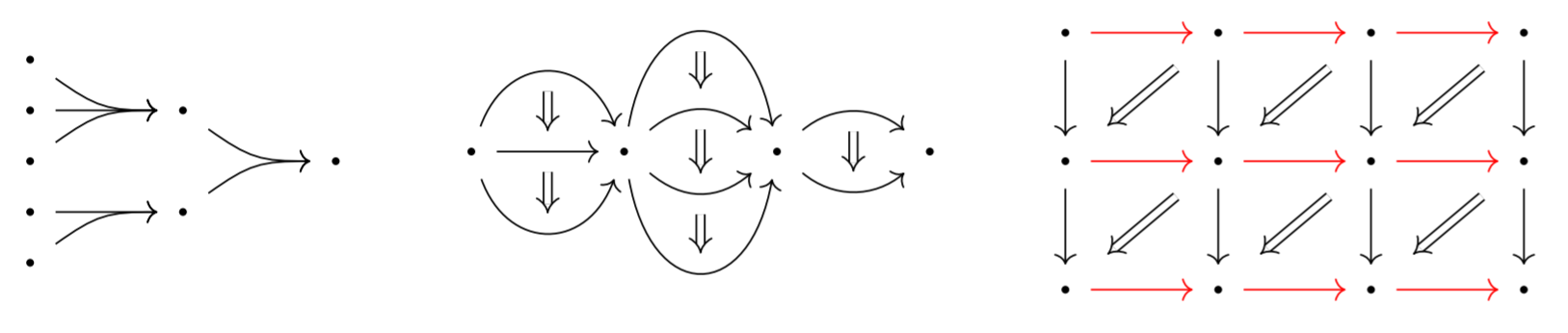
My thesis project is all about higher categories. Not the homotopy theorists’ kind of higher category, which is like a category that only follows the rules up to homotopy, but the algebraic kind which includes things like 2-categories, double categories, and multicategories. Each type of higher category has underlying cell shapes: some selection among dots, arrows, squares, lemon-shaped paths between arrows, many-to-one arrows, higher dimensional shapes, and countless more. These shapes come with strategies for composing them like successive arrows in a category, and equations between those compositions. Each type of higher category is encoded as algebras for a special kind of monad called “familial”, whose algebraic expressions are composable diagrams of cell shapes, and many features of category theory can be extended to more general kinds of higher categories. Hopefully, when new applications are found that require composing unexpectedly-shaped data in a new way, this new type of higher category will benefit from all the tools available in ordinary category theory.
At Topos I’m working with David Spivak on developing the theory and applications of polynomials, but I’ve actually been working with polynomials for a long time without realizing it. The category of polynomials contains all the information of the cell shapes and familial monads that define a type of higher category, which fits higher category theory into a beautiful ecosystem of pure and applied mathematics. Polynomials allow us to model human and computer activities in the same way I think about shapes and higher categories, and I’m very excited to see where it takes us.