Co-design of dynamical systems
In 2015, Andrea Censi invented a beautiful category-theoretic way to collaboratively and computationally design new things under complex systems of constraints. For example, suppose that a robot is made of a chassis and a motor. Since the motor powers the chassis and the chassis carries the motor, you could ask: is it worthwhile to use a more powerful motor, even if it weighs more?
In 2015, Andrea Censi invented a beautiful category-theoretic way to collaboratively and computationally design new things under complex systems of constraints. For example, suppose that a robot is made of a chassis and a motor. Since the motor powers the chassis and the chassis carries the motor, you could ask: is it worthwhile to use a more powerful motor, even if it weighs more?
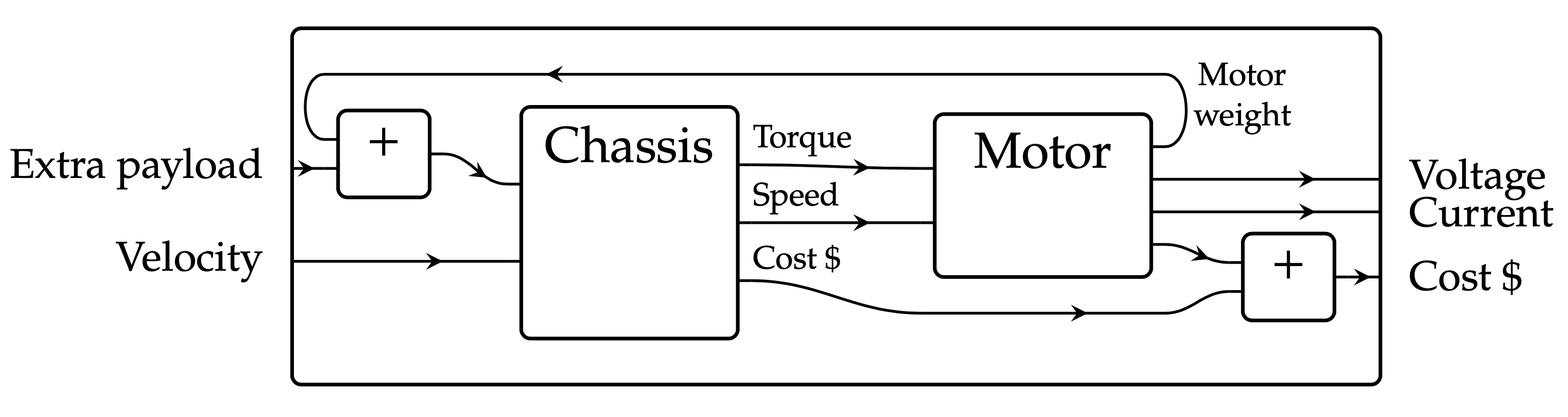
He called this system co-design. Below is a picture of a co-design problem, where a wire labeled f connecting boxes A and B means “A will get the f it needs from B”.
So here, the chassis gets its torque and speed from the motor, and both the robot extra payload and the motor are carried by the chassis. The whole robot gets its velocity from the chassis, and apparently the robot needs to provide voltage and current to the motor..? Oh, I guess that means this robot is missing a battery! We could hook a battery onto the battery-less robot, have the battery provide the voltage and current, and have the chassis carry the battery too. In other words, you can nest co-design problems inside co-design problems. Anyway, the whole story is worked out in (Censi: “A mathematical theory of codesign” [1]), and also in (Fong-Spivak: Invitation to applied category theory [2]).
In this post, I want to talk about a source of co-design problems. It comes from my recent work on interacting dynamical systems that rewire themselves based on what flows between them; see (Spivak: “Learners’ languages” [3]). The idea will be that invariant sets in dynamical systems will be resources, akin to voltage and speed above. I got the seed of this idea from Sophie Libkind, who’s thinking about such things too, and I’ve also benefited a lot from talking to Brandon Shapiro about neighboring ideas. Anyway, if we have an organization of little “worker” dynamical systems interacting in time-varying ways within a bigger “company” dynamical system, we can say when given invariant sets of the little systems, working together according to the organizational system, produce an output invariant that satisfies given requirements of the company.
The mathematics here is easy to state, if you already know the pieces. Namely it’s a lax monoidal bifunctor \mathrm{Inv}\colon\mathbb{O}\mathbf{rg}^\textnormal{co,op}\to\mathbb{P}\mathbf{oset}. I haven’t proved this works, so if you are interested in doing so, either go for it yourself (and please cite this blog post as inspiration), or contact me and we can work on it together. By the way, in case you’re saying “Oh dear, David said monoidal bicategory above, but everyone knows now that it’s easier to define monoidal fibrant double categories than monoidal bicategories”, don’t worry: both \mathbb{O}\mathbf{rg} and \mathbb{P}\mathbf{oset} come from monoidal fibrant double categories. And in case you’re saying “I have no idea what a monoidal double- or bi-category is”, then just aim at getting the big picture: I’m explaining to your future self a fairly easy-once-you-know-the-background idea, which says that we can make a co-design situation out of interacting dynamical systems.
So to tell you the idea, I need to remind you of what \mathbb{O}\mathbf{rg} and \mathbb{P}\mathbf{oset} are as monoidal bicategories. \mathbb{O}\mathbf{rg} is the story of interacting dynamical systems that change their interaction pattern; \mathbb{P}\mathbf{oset} is far more standard, but in fact it’s the story of co-design! Indeed, starting with the latter, \mathbb{P}\mathbf{oset} is the bicategory whose objects are posets P (we think of p\in P as a resource of type P and p\leq p' means that whenever we have p, we implicitly have p'), whose morphisms are bool-enriched profunctors, and whose 2-cells are maps of profunctors. The monoidal product is Cartesian product (P,Q)\mapsto P\times Q of posets.
The most important thing to understand about \mathbb{P}\mathbf{oset} is its morphisms, “bool-enriched profunctors”. Given posets P,Q a morphism \Phi\colon P{\;\;\;\mathclap{\,\,\longrightarrow}{\shortmid}\;\;\,\,}Q is defined to be a monotone map P^\textnormal{op}\times Q\to\{\texttt{False}<\texttt{True}\}. The idea is that elements of P are what they system \Phi is trying to provide, elements of Q are what the system \Phi will be offered for its use, and \Phi(p,q) says whether p can feasibly (or should I say \Phisibly?) be provided when offered q. The poset condition says that if p is feasible given q, and if having p means you implicitly have p' then p' is feasible given q. That is p'\leq p and \Phi(p,q) implies \Phi(p',q). Similarly reasoning says that \Phi(p,q) and q\leq q' implies \Phi(p,q'). So for example, the chassis designers say which Payload and Velocity they can feasibly provide when offered various amounts of Torque, Speed, and Cost: they give us a function that takes any ((p,v),(t,s,c)) and returns \texttt{True} if it’s feasible and \texttt{False} if not. Using the fact that \mathbb{P}\mathbf{oset} is appropriately compact closed, Censi implemented software called MCDPL that takes an arrangement of feasibility relations (profunctors), e.g. the inner boxes in Figure 1, and produce a feasibility profunctor, e.g. the outer box. It actually returns the “Pareto front” of all minimal resources needed to provide something you want.
Anyway, the second part of the background here is the story of \mathbb{O}\mathbf{rg}. Its objects are polynomial functors p in one variable, its morphisms are [p,q]-coalgebras, and its 2-cells are maps thereof. The monoidal product is Dirichlet product of polynomials (p,q)\mapsto p\otimes q.
The most important thing to understand about \mathbb{O}\mathbf{rg} is its morphisms. Given polynomials p,q, a morphism p{\;\;\;\mathclap{\,\,\longrightarrow}{\wr}\;\;\,\,}q is defined to be a coalgebra S\to[p,q]\mathbin{\triangleleft}S. Here [p,q] is the internal hom, i.e. the closure for \otimes; it has the following formula [p,q]\coloneqq\sum_{\varphi\in\mathbf{Poly}(p,q)}\mathcal{y}^{\sum\limits_{I\in p(1)}\;q[\varphi_1(I)]} That might be difficult to parse, but the idea is that the coalgebra is an organization of a p-dynamical system interacting inside of q-dynamical system, where this interaction pattern can change based on what flows. So for any state s\in S of this organization, we get a map \varphi\colon p\to q, which transforms outputs I\in p(1) of the inside “worker” dynamical system into outputs J\coloneqq\varphi_1(I) of the outer “company” dynamical system and transforms inputs j\in q[J] to the company into inputs \varphi^\sharp(I,j)\in p[I] of the worker. So for any state s, the organization transmits information back and forth between p inside and q outside. But that’s just what the organization does at any given moment; it also updates itself based on the pair (I,j) consisting of the current output I\in p(1) of the inner box and the current input j\in q[J] of the outer box, i.e. it uses this pair (I,j) to change its state from s to some new s'. To summarize, a morphism in \mathbb{O}\mathbf{rg} is a [p,q]-coalgebra S\to[p,q]\mathbin{\triangleleft}S, so it outputs interaction patterns, and changes these patterns based on what flows out of p and into q.
Finally, we get to the lax monoidal bifunctor \mathrm{Inv}\colon\mathbb{O}\mathbf{rg}^\textnormal{co,op}\to\mathbb{P}\mathbf{oset}, from the all-around opposite of \mathbb{O}\mathbf{rg} to \mathbb{P}\mathbf{oset}. Given any polynomial p, let \mathrm{Prop}(p)\in\mathbb{P}\mathbf{oset} denote the poset of subterminal p-coalgebras; Bart Jacobs calls these the p-behaviors. The idea is that these are dynamical systems with no duplicate, behaviorally-equivalent states. It forms a poset, and in fact a lattice, though we won’t use that. Following Sophie, we call its elements invariant sets, because this is a nice way to think of them: once you’re in one, you don’t leave. Now define \mathrm{Inv}(p)\coloneqq\mathrm{Prop}(p)^\textnormal{op}, so that B\preceq A means that A\leq B, the idea being that the invariant set A is more refined, more special, more particular, better constrained, than B. We made the choice to take the opposite—both on \mathbb{O}\mathbf{rg} and on each of the \mathrm{Prop}(p)’s—to say that inside “worker” things are given, and outside “company” things are needed, but you could reverse that; we took “co” here because we had to. The idea is that the behaviors of p are being thought of as resources, like wattage or money in Andrea’s usual setup, but here we think “human resources”. Something that is guaranteed to always behave a certain way is a useful resource.
The lax monoidality says that there is a map \mathrm{Inv}(p)\times\mathrm{Inv}(q)\to\mathrm{Inv}(p\otimes q); the idea is that an invariant set of p and an invariant set of q, isolated from each other, gives rise to an invariant set of p\otimes q. But the most important thing, as usual, is what happens on morphisms. Given a [p,q]-coalgebra S, we’re supposed to get a profunctor \mathrm{Inv}(q){\;\;\;\mathclap{\,\,\longrightarrow}{\shortmid}\;\;\,\,}\mathrm{Inv}(p), meaning that \mathrm{Inv}(q) is the poset of what’s needed by the company, \mathrm{Inv}(p) is the poset of what’s offered by the worker, and \mathrm{Inv}(S) tells us what our organization S makes feasible. Given B\in q\textnormal{-}\mathbf{Coalg} and A\in p\textnormal{-}\mathbf{Coalg}, we define \mathrm{Inv}(S)(A,B) to return true if (A\mathbin{;}S)\subseteq B, i.e. if B\preceq (A\mathbin{;}S), which means that the resource A\mathbin{;}S is more refined, better constrained, than the required B. Of course, if B'\preceq B and A\preceq A' then B\preceq(A\mathbin{;}S) implies B'\preceq (A'\mathbin{;}S), so \mathrm{Inv}(S) is a profunctor. Given a morphism S\to S' in [p,q]\textnormal{-}\mathbf{Coalg}, we need a map of profunctors \mathrm{Inv}(S')\to\mathrm{Inv}(S), meaning that if S' makes something feasible then so should S. Mathematically, (A\mathbin{;}S)\subseteq(A\mathbin{;}S') so that indeed (A\mathbin{;}S')\subseteq B implies (A\mathbin{;}S)\subseteq B. To use Sophie’s summary of \mathrm{Inv} on morphisms, \mathrm{Inv}(S)(A,B) is true if the following holds: “given A-invariants on the behavior of the workers, and given the interaction pattern S, then the B-invariants on the behavior of the CEO will be satisfied.”
So that’s the story! We can take changing organizational interaction patterns and obtain a co-design problem in the sense of Censi, so that plugging dynamical systems to the interior interface generates desired behaviors on the exterior interfaces. It would be neat if Censi’s MCDPL software could be used effectively in this context to search for ways of constructing new behaviors from old. Maybe in the future!