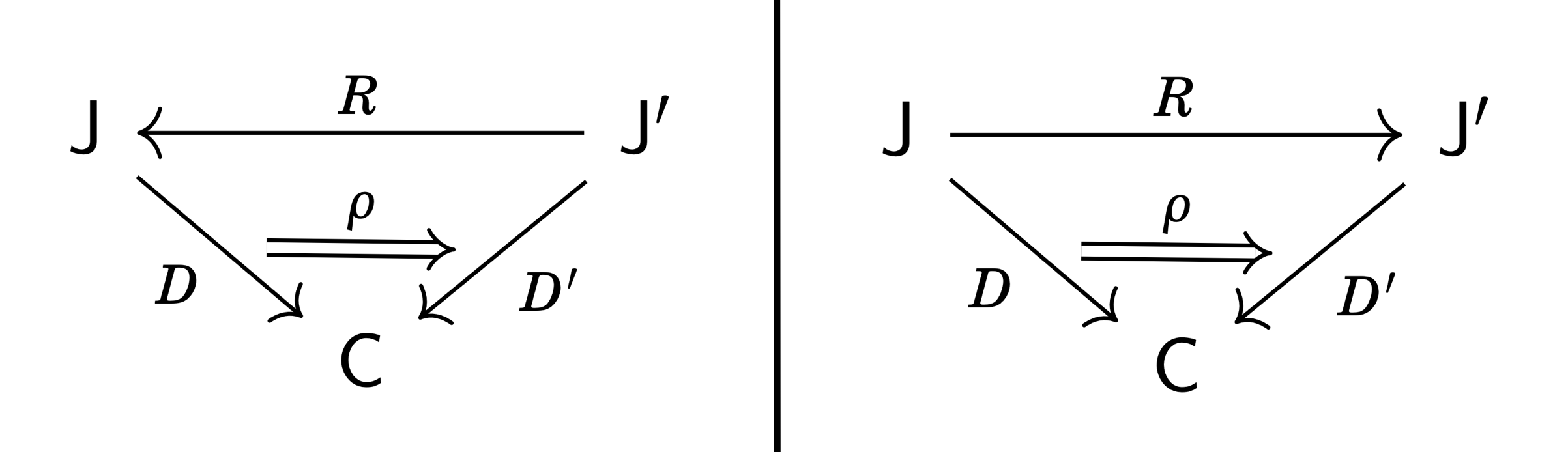Diagrammatic equations and multiphysics (Part 1)
Using diagrams to encode equations between physical quantities is something that has become more and more common over the past few decades. To a category theorist, however, the use of such diagrams is not as formal as one would perhaps like. In this new paper, we fix this problem: systematising the use of diagrams in expressing multiphysics models and their solutions via a categorical framework.
(See Part 2 of this series here)
One of the things that I (Tim) really like about working with Topos, from a personal aspect, is the wealth of interdisciplinary research opportunities that it presents. For example, a while back now, Evan messaged me to ask some questions about sheaves in differential geometry and the discrete exterior calculus (things that I know at least a little bit about), and explained to me why he was interested in them: he was working with Andrew Baas and James Fairbanks on things called Tonti diagrams — a diagrammatic way of presenting equations in physics — and trying to formalise them in the language of category theory. So our conversations went back and forth, with Evan explaining things to me and me trying to do the same back, and I eventually ended up writing up a small bunch of stuff about localisation via calculi of fractions and weak equivalences and many such things that I’ve already talked a bit about on this blog before. As often happens, this section ended up growing too long and disjoint from the original path of the paper that he, Andrew, and James were writing, so we removed most of it, stashed it away for future work, and thoughtfully scattered the most important and relevant bits throughout the rest of paper.
But this blog post isn’t about that at all — this blog post is about the paper itself, and all the things that are in it (and there are lots of things in it!). For those of you who would rather just dive in, here’s a link to the paper:
Evan Patterson, Andrew Baas, Timothy Hosgood, James Fairbanks. “A Diagrammatic View of Differential Equations in Physics.” arXiv:2204.01843
Abstract. Presenting systems of differential equations in the form of diagrams has become common in certain parts of physics, especially electromagnetism and computational physics. In this work, we aim to put such use of diagrams on a firm mathematical footing, while also systematizing it into a broadly applicable framework for formal reasoning about systems of equations and their solutions. Our main mathematical tools are category-theoretic diagrams, which are well known, and the morphisms between them, which have been less appreciated. As an application of the framework, we show how complex, multiphysical systems can be modularly constructed from basic physical principles. A wealth of examples, drawn from electromagnetism, transport phenomena, fluid mechanics, and other fields, is included.
But for those of you who would appreciate a short summary, read on! This is will be the first of two posts: here we’ll explain how diagrams are actually useful for talking about systems of equations and their solutions; in the next part, we’ll look at how we can extend the framework to express more complex equations.
(N.B. I’ll include some citations but not a bibliography, so for proper references see the full paper on the arXiv.)
1 Equations as diagrams
(A quick note before we dive in: we’re going to look at some examples in electromagnetics, fluid dynamics, and some other physics-y areas, but I really want to stress that you don’t have to know anything about these areas in order to understand what we’re talking about. If it helps, you can just take for granted that the equations describe something interesting.)
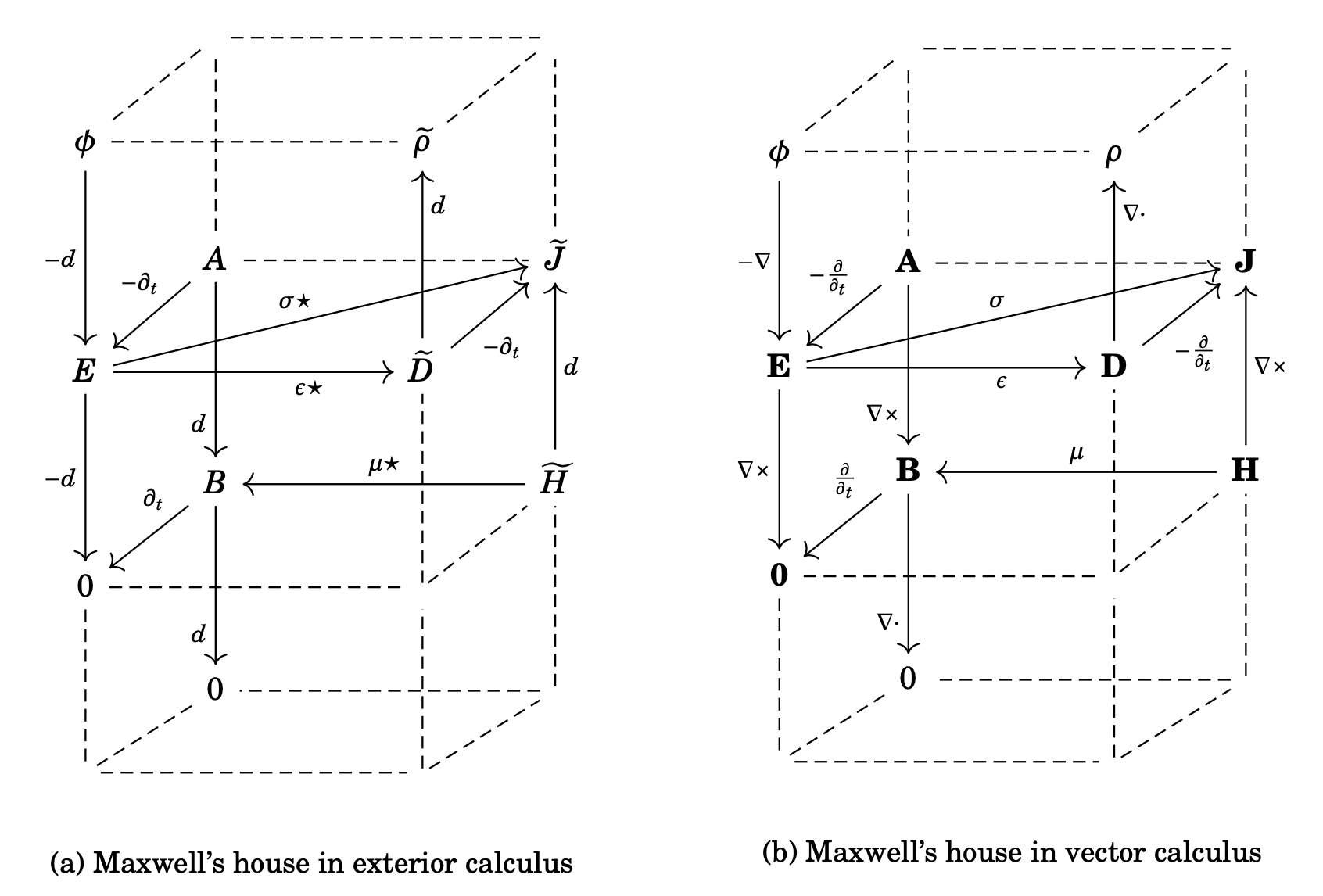
Probably the most famous example of diagrammatic presentations of physical theories is the so-called Maxwell’s house, which present Maxwell’s equations for electric and magnetic fields. We give two reproductions of Maxwell’s house in Figure 1, but we should really explain how you’re meant to read them.
Loosely speaking, such diagrams are directed graphs, where the nodes represent physical quantities (such as fields or densities) and the arrows represent equations between the physical quantities. Let’s try to be a bit more precise about how to read these diagrams and, in the process, reveal why a more careful formalisation is needed.
- A single arrow f\colon x\to y asserts the equation “f(x)=y”. For example, in Figure 1 (a), the vertical arrow d\colon A\to B tells us that the magnetic field B (a 2-form) and the magnetic potential A (a 1-form) are related by the equation dA=B (where d is the exterior derivative).
- Multiple arrows pointing to the same node represent a sum of values. For example, the pair of arrows -d\colon\phi\to E and -\partial_t\colon A\to E in Figure 1 (a) encodes the equation E=-d\phi-\partial_t A (relating the electric field E with the electric potential \phi and the magnetic potential A).
But here we already encounter a problem with consistency: in Figure 1 (a) we see that the current density \widetilde{J} has three incoming arrows, which should represent the equation \widetilde{J}=\sigma\star E-\partial_t\widetilde{D}+d\widetilde{H}, but that equation is wrong! Instead, the intended parsing is to split the three arrows into two “families”, one encoding the equation \widetilde{J}=\sigma\star E, and the other encoding \widetilde{J}=-\partial_t\widetilde{D}+d\widetilde{H}. Tonti avoids this inconsistency in his version of Maxwell’s house (cf. Diagram ELE3 in The mathematical structure of classical and relativistic physics) but only through an even more informal use of diagrams. That is not necessarily a problem: informal diagrams can be useful as a visual and intuitive aid in understanding how a specific physics model is built up from smaller parts. Our goal, however, is to turn these diagrams into formal, systematic tools that have precise and unambiguous interpretations.
2 A nice example
There are lots of interesting details about how we can encode differential-geometric information in diagrams presenting equations, but I’m going to avoid talking about that here, since it really deserves a proper explanation. It also leads to questions about discretization and computer implementation, such as how discrete exterior calculus can be used and how one might define operators like the Hodge star in a discrete setting. So, for the sake of this blog post, our main example will be a linear difference equation instead of a differential equation. Let’s get to the setup!
Recall that a symmetric weighted graph is a diagram of sets and functions V \overset{s}{\underset{t}{\leftleftarrows}} \overset{\overset{i}{\curvearrowright}}{E} \overset{\mu}{\rightarrow} \mathbb{R}_{>0} where s and t are the source and target maps, i is the edge involution, and \mu is the edge weight; this data must satisfy the equations i^2=\mathrm{id}_E, is=t, it=s, and i\mu=\mu. Symmetric graphs are very nice mathematical objects, which can be easily implemented using Catlab. With this definition, time-dependent real-valued functions on the vertices of a symmetric weighted graph G=(V,E,s,t,i,\mu) are vectors u\in\mathbb{R}^{\mathbb{N}\times V}, i.e., real-valued functions u\colon\mathbb{N}\times V\to\mathbb{R}.
How can we present this equation as a diagram? Well, consider the diagram \mathbb{R}^{\mathbb{N}\times V} \;\overset{\partial_n}{\underset{\Delta}{\rightrightarrows}}\; \mathbb{R}^{\mathbb{N}\times V} \tag{$\circledast$} i.e., a diagram D\colon\mathsf{J}\to\mathsf{Vect}_\mathbb{R} in the category of real vector spaces whose shape \mathsf{J}\coloneqq\langle\bullet\rightrightarrows\bullet\rangle is the free category on two parallel arrows.
Now, the fundamental insight, which is perhaps surprising to those of us who are used to hearing about diagrams in category theory, is that we do not want our diagrams to commute. If the diagram (\circledast) commuted then this would say that every choice of u\in\mathbb{R}^{\mathbb{N}\times V} satisfies \partial_n u=\Delta u, which is not what we want! Instead, we need to find a formal way to express the idea that the diagram does not commute in general, but “does for certain elements,” namely the solutions of the equation. To do this, we need to understand lifting problems and generalised elements.
- Given a diagram D\colon\mathsf{J}\to\mathsf{C} and a functor \pi\colon\mathsf{E}\to\mathsf{C}, the associated lifting problem is to find a diagram \overline{D}\colon\mathsf{J}\to\mathsf{E} such that D=\pi\circ\overline{D}.
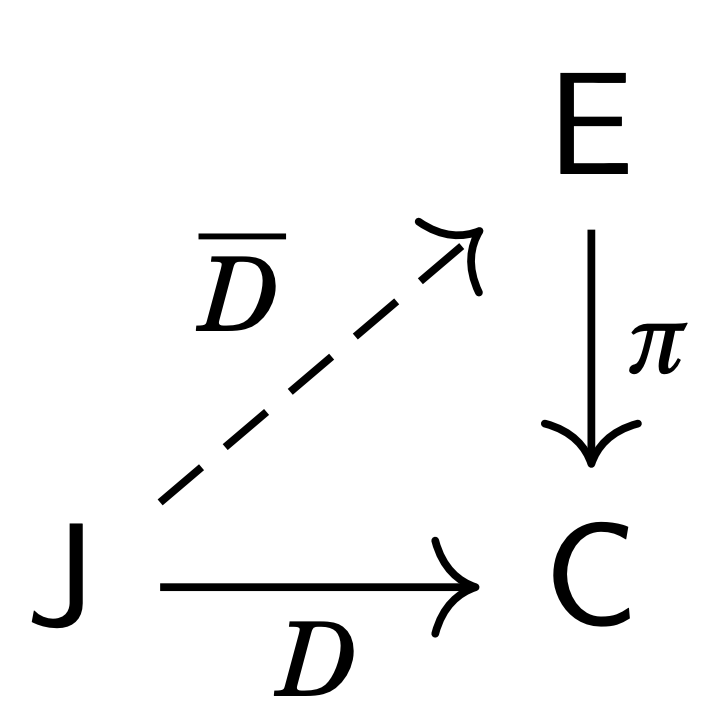
- Given a category \mathsf{C} and an object S\in\mathsf{C}, a generalised element of shape S of \mathsf{C} is a morphism x\colon S\to X in \mathsf{C}. These assemble into the coslice category S/\mathsf{C}, which we will thus refer to as the category of generalised elements of shape S, denoted \mathrm{El}_S(\mathsf{C}).
So how are these two definitions useful? Well, it turns out that solving an equation presented by a diagram corresponds to solving the lifting problem of the diagram through to the codomain functor \pi=\operatorname{cod}\colon\mathrm{El}_S(\cal{C})\to\cal{C}. (Some further category-theoretic yoga tells us that lifts of a diagram D\colon\mathsf{J}\to\cal{C} through \operatorname{cod}\colon\mathrm{El}_S(\cal{C})\to\cal{C} are exactly cones over D with apex equal to S, which can motivate how limits of diagrams give “universal solutions” to the presented equations.)
For example, a lift of the diagram (\circledast) to \mathrm{El}_\mathbb{R}(\mathsf{Vect}_\mathbb{R}) consists of vectors u,\dot{u}\in\mathbb{R}^{\mathbb{N}\times V} such that \begin{aligned} \partial_n u &= \dot{u} \\\Delta u &= \dot{u} \end{aligned}, which is equivalent to a single vector u\in\mathbb{R}^{\mathbb{N}\times V} satisfying the discrete heat equation!
We can now be a little loose and suggestive with our notation: similar to how an equation like “f(x)=y” could mean either that x and y are indeterminates, waiting to be filled in, or that they are specific values that satisfy the equation, we can write the diagram (\circledast) as u:\mathbb{R}^{\mathbb{N}\times V} \;\overset{\partial_n}{\underset{\Delta}{\rightrightarrows}}\; \dot{u}:\mathbb{R}^{\mathbb{N}\times V} leaving it deliberately ambiguous as to whether this is a diagram in \cal{C} or in \mathrm{El}_S(\cal{C}).
3 Morphisms of diagrams
Something that seems to have been overlooked in the literature on diagrammatic approaches to presenting equations is the fact, long known but arguably underappreciated, that diagrams in a given category themselves form a category (in two different ways).
Given a category \mathsf{C}, we define the category \mathrm{Diag}_\leftarrow(\mathsf{C}) as follows:
- its objects are diagrams D\colon\mathsf{J}\to\mathsf{C} in \mathsf{C}, which we write as (\mathsf{J},D);
- its morphisms (\mathsf{J},D)\to(\mathsf{J}',D') are pairs (R,\rho), where R\colon\mathsf{J}'\to\mathsf{J} is a functor going “in the backward direction” and \rho\colon D\circ R\Rightarrow D' is a natural transformation.
Dually, we define \mathrm{Diag}_\rightarrow(\mathsf{C}) in the same way, but with the functor part of morphisms going “in the forward direction.” Thus, a morphism (\mathsf{J},D)\to(\mathsf{J}',D') in \mathrm{Diag}_\rightarrow(\mathsf{C}) is a pair (R,\rho) where R\colon\mathsf{J}\to\mathsf{J}' and \rho\colon D\Rightarrow D'\circ R.
We say that a morphism (R,\rho) in either diagram category is strong if \rho is a natural isomorphism, and strict if \rho is an identity. This means that, if we just consider strict morphisms in \mathrm{Diag}_\rightarrow(\mathsf{C}) (resp. \mathrm{Diag}_\leftarrow(\mathsf{C})), then we recover the slice category \mathsf{Cat}/\mathsf{C} (resp. its opposite (\mathsf{Cat}/\mathsf{C})^\mathrm{op}).
(Our choice of notation (using \leftarrow and \rightarrow) is intended to be suggestive: there turns out to be a natural way of getting functors \lim=\lim_\leftarrow\colon\mathrm{Diag}_\leftarrow(\mathsf{C})\to\mathsf{C} and \operatorname{colim}=\lim_\rightarrow\colon\mathrm{Diag}_\rightarrow(\mathsf{C})\to\mathsf{C}, and this links back to our previous comment about how limits correspond to universal solutions. To tell this whole story in detail spans a few sections of the paper, and relies on the notion of discrete opfibrations, so I’m not going to even try to summarise it here — go read the paper!)
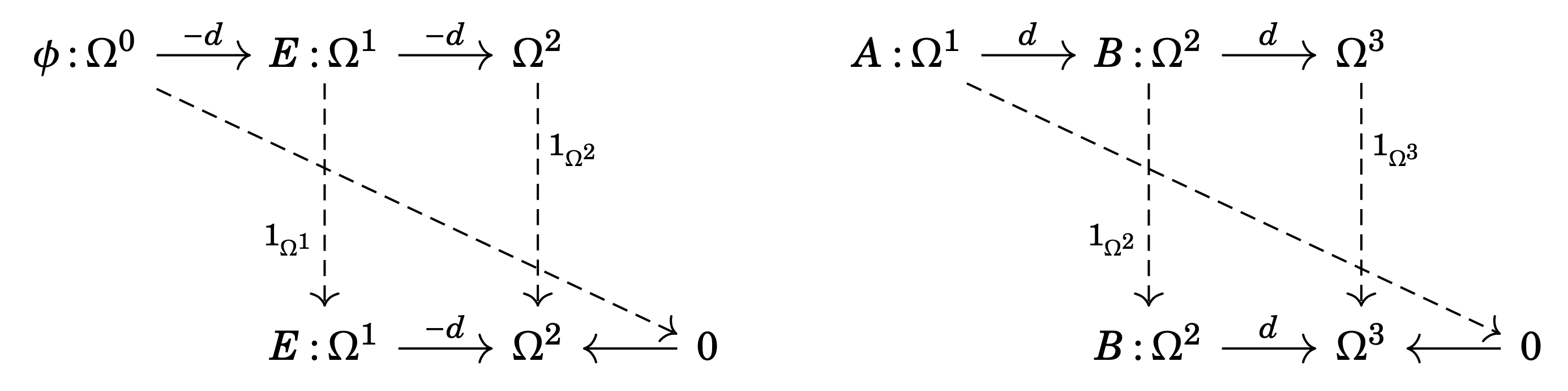
There is an “obvious” morphism from diagram (\circleddash) to diagram (\circledcirc), which we can draw by specifying the components of the natural transformation, as shown in Figure 3. You might note that the morphism goes in the direction of increasing generality (or decreasing specificity), i.e., the existence of the potentials \phi and A implies that dE=dB=0, but the converse does not hold. In other words, for those who prefer this language: all exact forms are closed, but not all closed forms are exact.
Now we arrive at a natural question: what do morphisms of diagrams tell us? More specifically, we might ask: what does it mean for two diagrams to be isomorphic? The answer is that, for most purposes, the notion of isomorphism of diagrams is too strict to be useful.
In Example 4.6 in the paper, we discuss the heat equation, and give two diagrams that present it; there is a strict morphism from one to the other. In fact, the two diagrams are “equivalent” in a very natural way: any solution of one gives a corresponding solution of the other. Yet the strict morphism between them is not an isomorphism. Even worse, it’s not a 2-categorical equivalence (when the category of diagrams is given its proper status as a 2-category). This situation gives us two things to think about:
- When should we consider two physical theories to be “the same”? Is “they have the same solutions” really the best definition?
- Is there a sense in which the strict morphism between the two presentations of the heat equation can be considered an equivalence?
The first question is out of the scope of our paper, being aimed more towards philosophers of science. The second question, however, does have a nice (partial) answer: we can introduce a “homotopical” notion of weak equivalence of diagrams, capturing the idea that “two diagrams with solutions sets in bijection with each other should be equivalent.” This is something that we will return to later, since it requires a bit more category theory.
For now, let me just mention another use of morphisms of diagrams: they let us formulate boundary value problems (which, in our framework, include initial value problems as a special case) as extension-lifting problems of diagrams, generalizing the lifting problem of diagrams described earlier. Of course, we walk through the details of this in the paper.
In summary, diagrams and their morphisms give us a solid theoretical framework with which to describe systems of equations and their solutions. In the next part of the post we’ll talk about how we can go even further in this theory, allowing us to deal with more complicated equations, and how to compose them together to describe multiphysics systems. We’ll also look at how to formalise this notion of “weak equivalence”, and how it leads to the definition of relatively initial functors.
See you next time!