Diagrammatic equations and multiphysics (Part 2)
Previously, we surveyed some of the fundamental concepts from our paper on the use of diagrams to present equations from mathematical physics. In this blog post we take a look at how we can enrich our framework, introducing cartesian and symmetric monoidal products in order to be able to express more complicated (e.g. non-linear) systems of equations. We also take a look at how we can use undirected wiring diagrams to build up multiphysics models from smaller constituent pieces. Finally, we have a look at some of the interesting questions in pure category that arise from this subject.
(See Part 1 of this series here)
In the previous blog post in this diptych on our recent preprint “A diagrammatic view of differential equations in physics”, we saw how the category of diagrams gives us a formal way to describe equations and their solutions. In this second and final part, we’re going to see how cartesian products and tensor products can help us to express more complicated equations, and then how we can piece together smaller equations, as building blocks, to get bigger equations describing multiphysics systems. We’ll end with some pure category theory, trying to find a “good” notion of equivalence for diagrams and seeing how this leads us to the definition of relatively initial functors.
Without any further ado, let’s pick up where we left off last time.
1 Cartesian and tensor products
The few examples of physical theories we gave last time were all pretty simple, which was not a coincidence. If we want to talk about more complicated equations, such as those involving sums or multilinear functions, then we need to extend our framework beyond the very fundamentals of category theory (categories, functors, and natural transformations) and introduce more structure. We’ll start with cartesian products.
For us, a cartesian category is a category with finite products (note that this departs from some other authors, who use the term to mean “category with all finite limits”), and a cartesian functor between two cartesian categories is a functor that preserves finite products. Putting it all together, we get the notion of a cartesian diagram, which is simply a cartesian functor from a small cartesian category \mathsf{J} to a cartesian category \mathsf{C}. Thankfully, any category of generalised elements of a cartesian category is itself a cartesian category, and the codomain functor \pi\coloneqq\operatorname{cod}\colon\mathrm{El}_S(\mathsf{C})\to\mathsf{C} is a cartesian functor. This means that we can (after checking a few technical details) take our whole framework of lifting problems and extension-lifting problems and just put the word “cartesian” in front of everything.
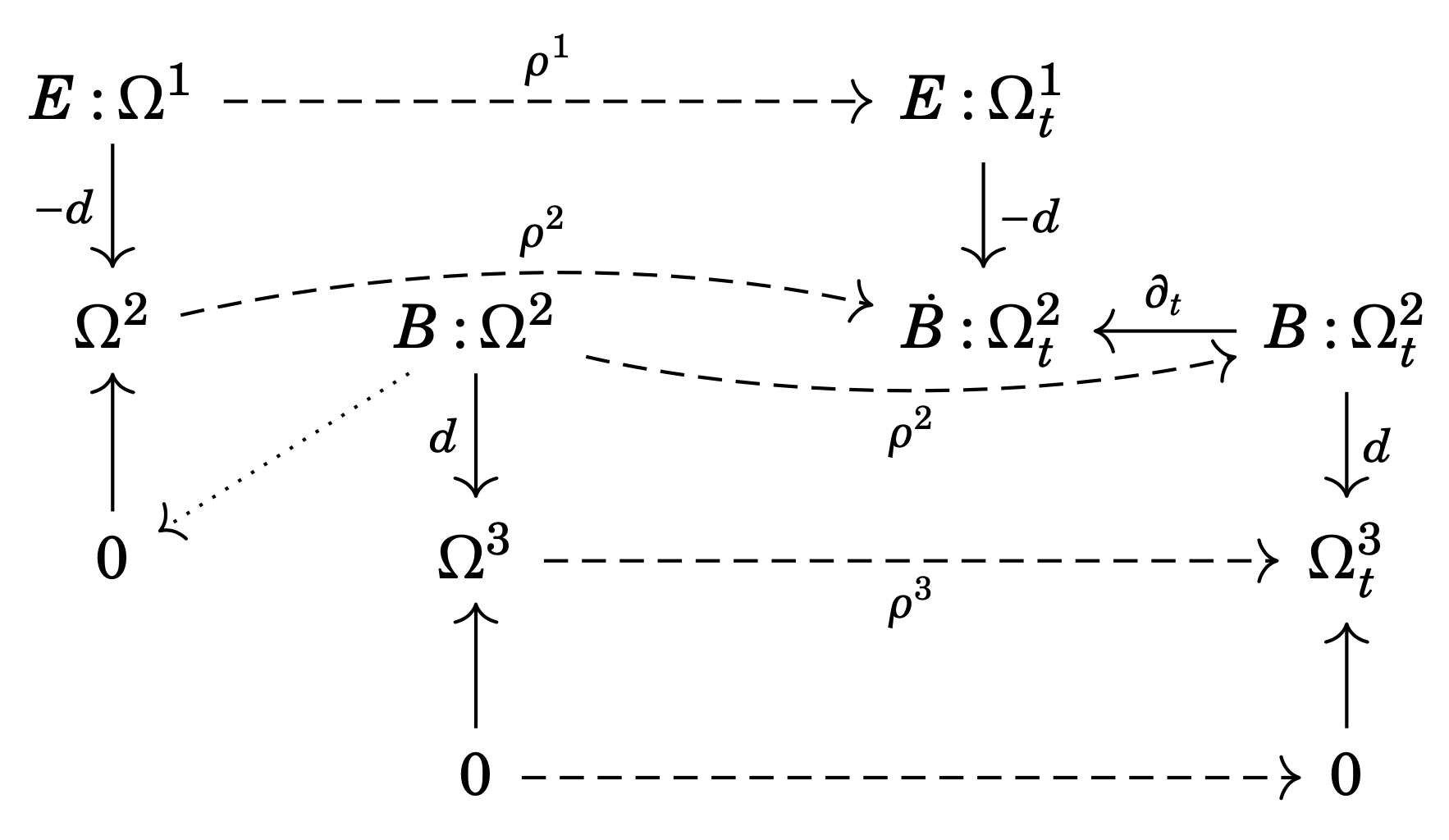
To see how this is useful, let’s revisit an example from the previous blog post, the Maxwell–Faraday equations, along with their extension to the full set of Maxwell’s equations.
Any solution of the static Maxwell–Faraday equations can be thought of as a solution of the dynamic Maxwell–Faraday equations that happens to be static in time. Following the intuition developed in the previous post, we would therefore expect to obtain a morphism of diagrams \circledcirc_\mathrm{s}\to\circledcirc_\mathrm{d}, i.e., from the static case to the dynamic case. This is indeed the case if the diagrams are taken to be cartesian, since the indexing category needs to “know” that the zero vector space is terminal. The diagram morphism is shown in Figure 1.
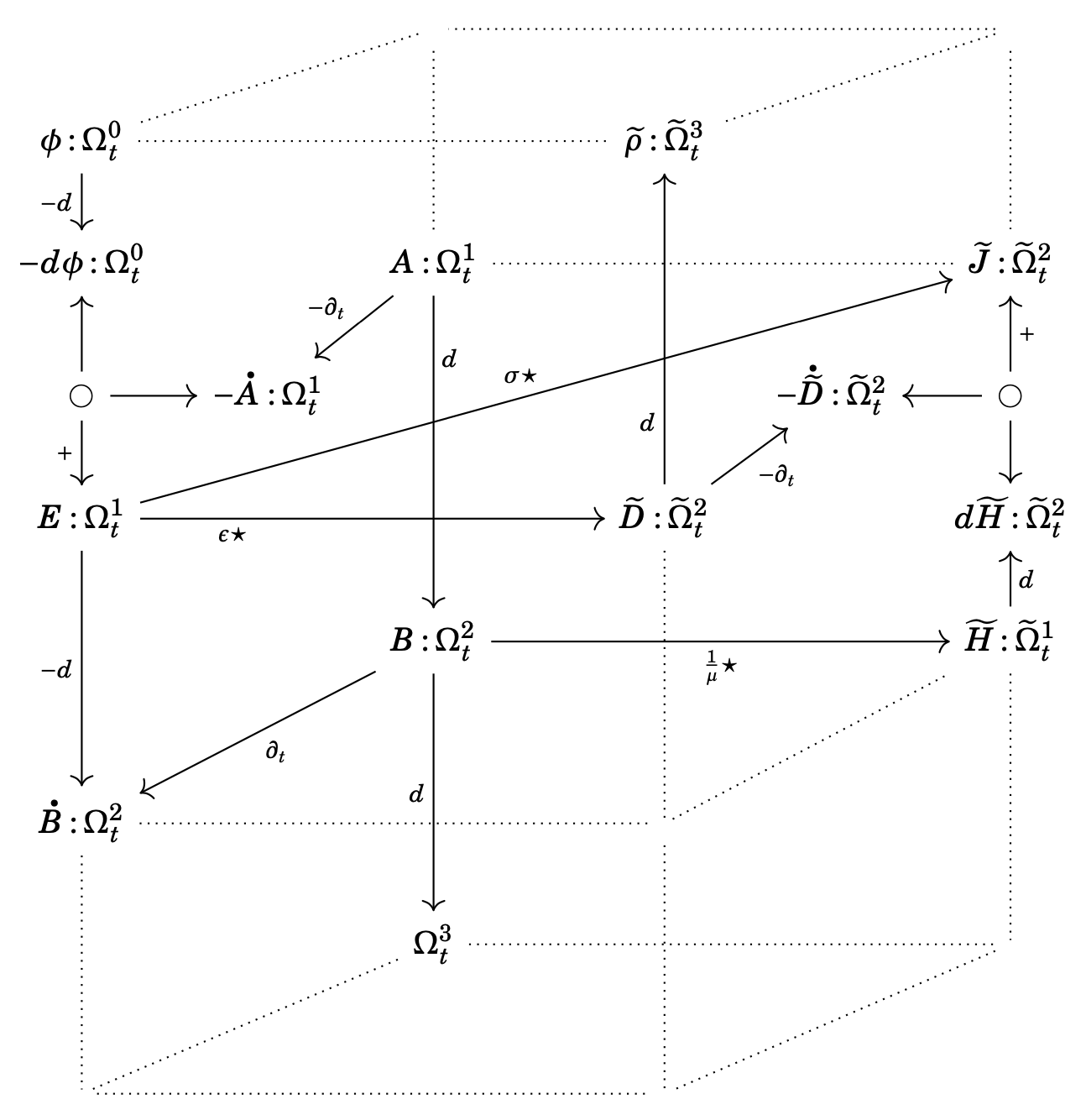
Using the language of cartesian diagrams, we can also finally draw a formal version of Maxwell’s house, as promised at the very start of this exposition!
Before moving on from products, it is important to mention another generalisation that we can make. Any physical systems modelled by linear partial differential equations can be formalised using cartesian products, but what about non-linear systems?
If the system is really non-linear (e.g. the sine-Gordon equation), then we must leave behind the category of (sheaves of) vector spaces and linear maps and instead work in the category of (sheaves of) sets and functions. But “most” equations that one encounters in mathematical physics are much more structured than an arbitrary non-linear system: they might be non-linear, but they are at least multilinear in the unknown functions and their derivatives. Now we can turn to linear algebra for a solution: there is a tool for turning multilinear functions into linear ones, the well loved tensor product.
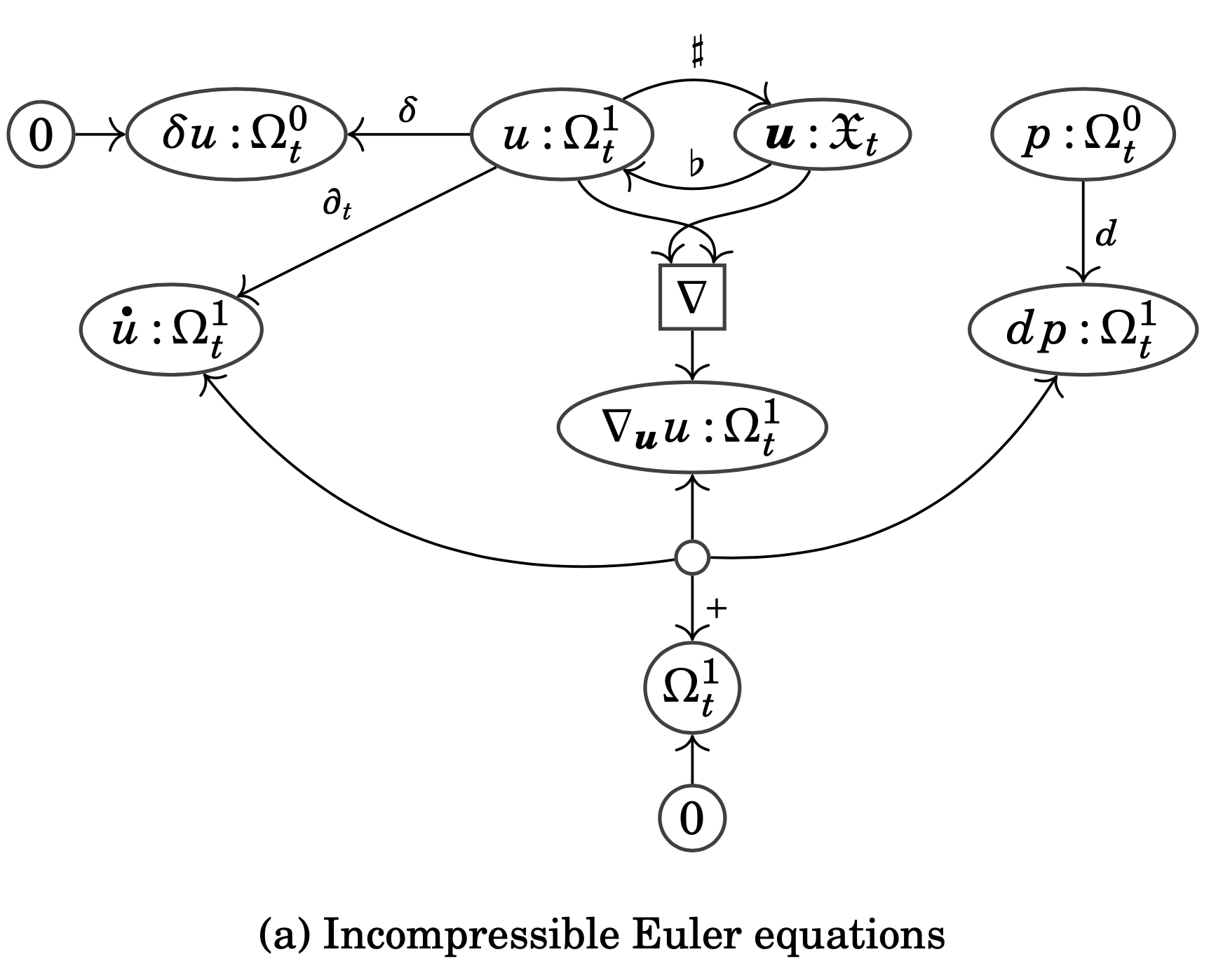
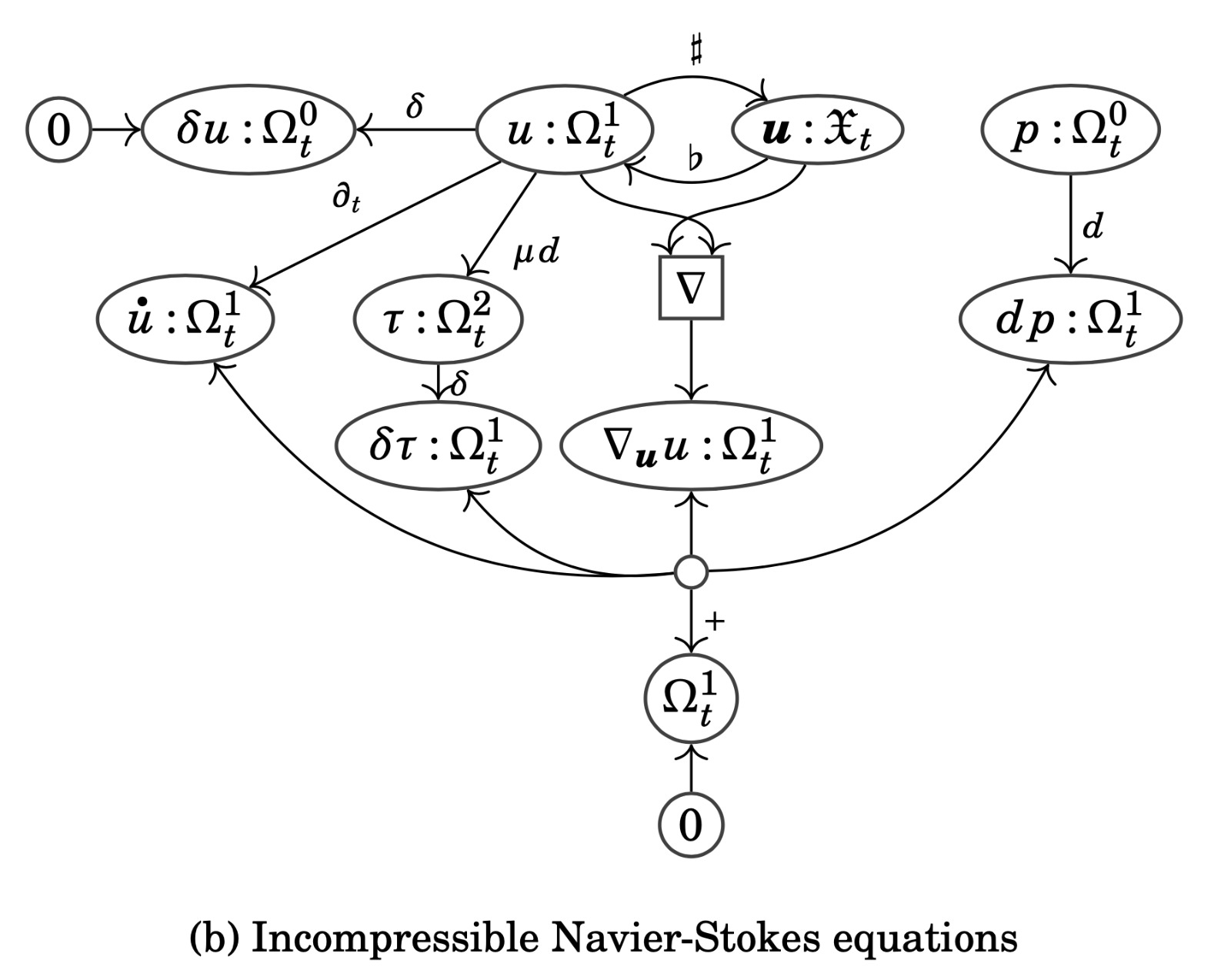
As we did for cartesian products, we can try to enrich our entire framework with the structure of symmetric monoidal products, working with symmetric monoidal functors between symmetric monoidal categories and monoidal transformations between those. Although this is possible (and explained in our paper), the conceptual leap from cartesian diagrams to symmetric monoidal diagrams is actually quite a bit bigger than the previous leap from bare diagrams to cartesian diagrams. Moreover, in practice, the leap is made bigger still by needing to consider both kinds of products together, leading to the general notion of symmetric rig categories. Because of this, I won’t go into any of the details here, and instead content myself with showing two symmetric monoidal diagrams that we construct, both describing the flow of an incompressible fluid on a Riemannian manifold. You will notice that these diagrams look different from the previous ones. That is because we are now working with a variant of Petri nets suitable for presenting free symmetric monoidal categories, namely \Sigma-nets or whole-grain Petri nets.
2 Composition for multiphysics
When we consider physical systems that we wish to model, we realise that they are often built up from smaller distinct physical phenomena. For example, a reaction-diffusion system is, as the name suggests, a system which experiences both chemical reactions between its different substances as well as simultaneous diffusion of those substances throughout a medium. Of course, one can ask how many turtles we need: the diffusion process, for example, arises from the conjunction of several other distinct physical principles, so what really are the fundamental building blocks of a reaction-diffusion system?
This philosophical question aside, in order to talk about composition of systems, we need to introduce two more concepts: open diagrams (which we define to be a specific type of structured spans) and undirected wiring diagrams, where the latter is the thing we use to compose together the former. Again, for technical details see the paper; our goal in this blog post is to just gain some familiarity with these things through examples.
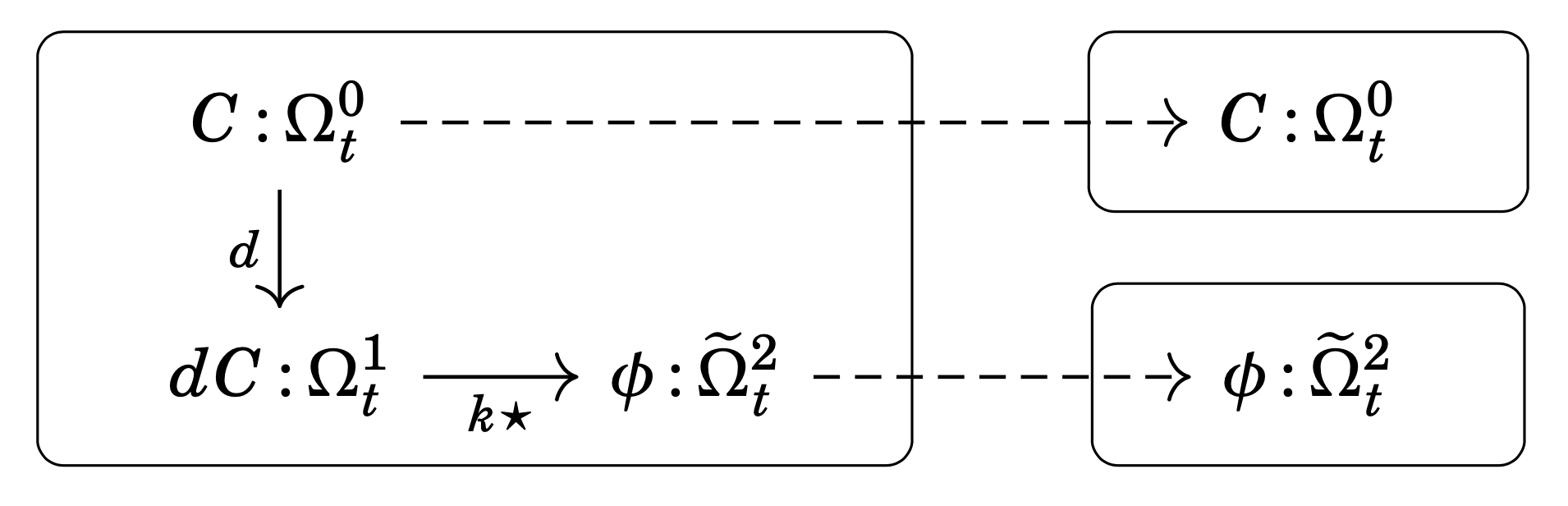
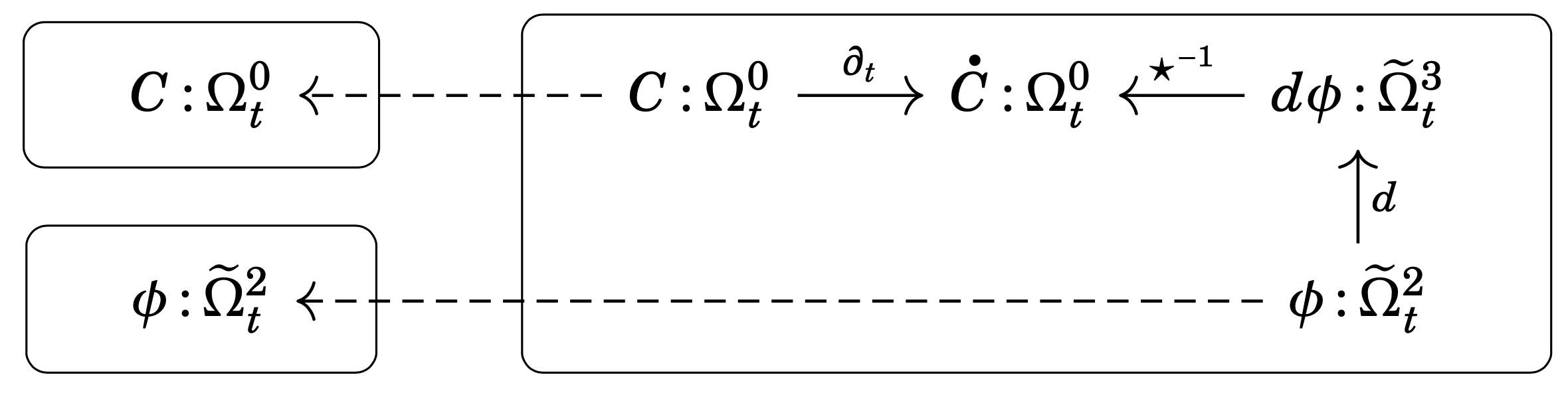
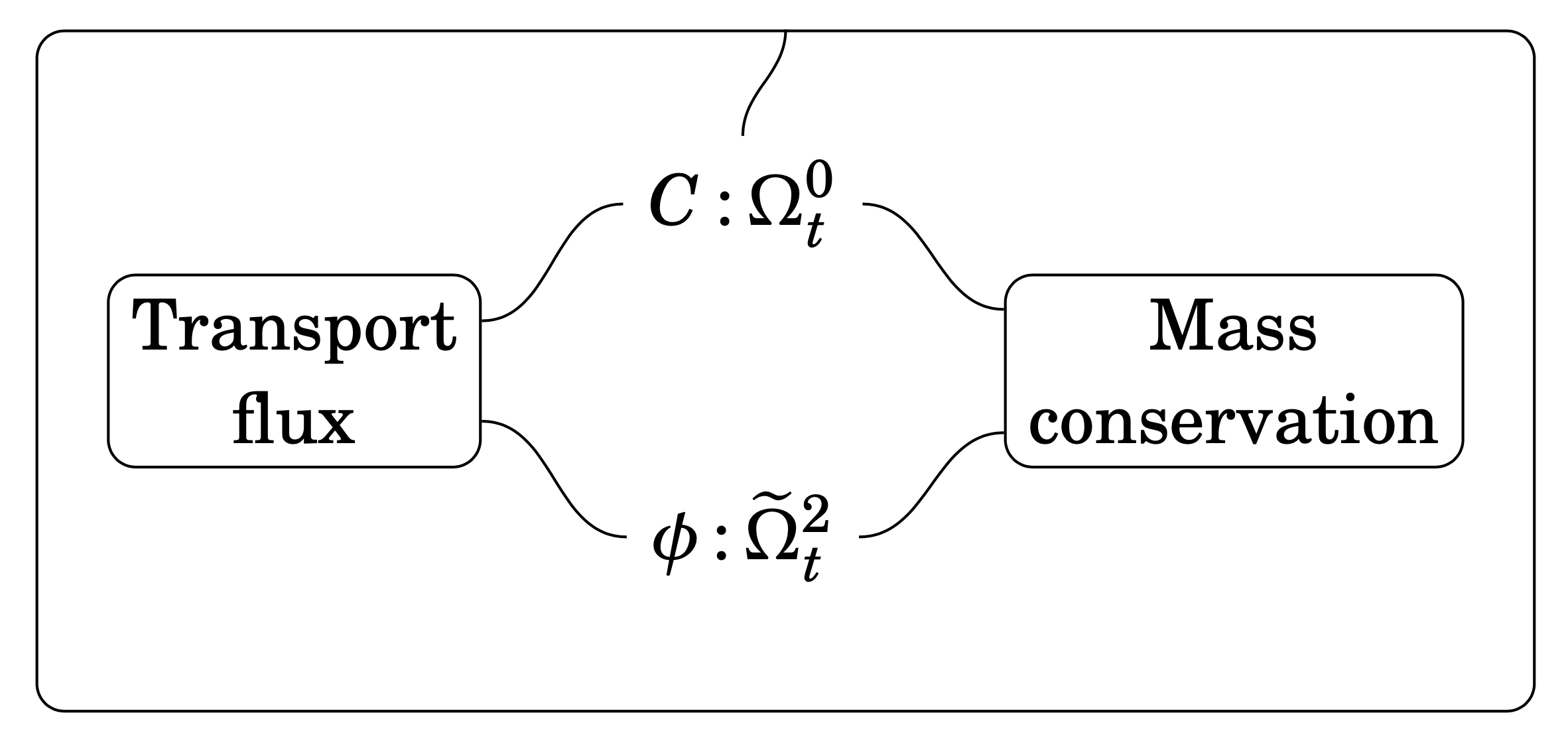
As hinted by the above description, the diffusion equation arises as a combination of an experimental law governing the transport process (Fick’s first law) with a conservation principle (conservation of mass). Without worrying too much about what we’re doing formally, we can split up the diagram in (\oslash) into three parts: two physical principles (transport flux and mass conservation) and one “rule for composition”. Doing so, we obtain the open diagram for Fick’s first law (Figure 5), the open diagram for conservation of mass (Figure 6), and the undirected wiring diagram expressing the relation between these two principles and the concentration C and (negative) diffusion flux \phi (Figure 7).
Hopefully, even if you have no idea what structured spans or undirected wiring diagrams are, these figures will make some sort of sense as a way to express the composite system (the diffusion equation) in terms of two smaller systems (Fick’s first law and conservation of mass) along with the information of how to combine them (the undirected wiring diagram).
Not only does this compositional approach to physical theories allow us to visualise the constituent parts, it also gives us a modular framework: we can swap out or extend any of the building blocks to obtain a different result. For example, we might have a physical scenario where the substance being diffused is simultaneously being transported by a moving fluid, known as an advection-diffusion or convection-diffusion system. To model this scenario, we need only replace the open diagram that we plug into the “transport flux” box of Figure 7: instead of using only Fick’s first law, we supply an open diagram giving the flux due to both diffusion and advection — the rest of the ingredients are unchanged! This example is worked out in detail in the paper.
3 Bonus category theory and future work
I don’t want to make this blog post any longer than it already is, so I’ll keep this section brief, but I at least want to mention some interesting bits of pure category theory that come up in the paper. As we saw last time, the notion of equivalence of diagrams is subtle, but a reasonable candidate definition is that “two diagrams are equivalent if the solutions to the equations they present are in one-to-one correspondence.”
Somewhat more formally, we say that a morphism (R,\rho): D \to D' in the diagram category \mathrm{Diag}_\leftarrow(\mathsf{C}) is a weak equivalence if it is strong (i.e., \rho is invertible) and if the morphism (R,\rho^{-1}): D' \to D in \mathrm{Diag}_\rightarrow(\mathsf{C}) has the property that, for nice enough functors \pi\colon\mathsf{E}\to\mathsf{C}, any lift of the diagram D' through \pi can be uniquely transported along (R,\rho^{-1}) to a lift of D. Of course, to make this precise, we need to say what “nice enough” means — it turns out that discrete opfibration is the right concept.
But the important question for any concrete situation is: how can we tell when a specific diagram morphism has this lifting property? There turns out to be a sufficient, but not necessary, condition, namely that R be an initial functor. “What”, you might then ask, “is an initial functor?”, to which I reply “I’m not going to tell you, but here are three sufficient conditions for a functor to be initial”:
- essentially surjective full functors are initial;
- composites of initial functors are initial;
- equivalences of categories are initial.
The reason that I don’t want to tell you the (admittedly rather succinct) definition of an initial functor is that it won’t be immediately clear why it is a sufficient condition for a diagram morphism to be a weak equivalence. There is, however, a “proposition-definition” of initial functors, which I will state here because it provides useful intuition. Recall, from the previous blog post, that solutions to equations presented by diagrams correspond to cones, and thus limits have some relevance to our topic.
Again, however, the functor part R of a diagram morphism (R,\rho) being initial is a sufficient but not necessary condition for the morphism to be a weak equivalence. We give a simple example showing why in the paper. Somehow this boils down to the fact that initiality is a syntactical property, having only to do with the diagrams’ indexing categories. That is, it relies on the shapes of the diagrams (the categories \mathsf{J}) but not on the actual data of the diagrams (which live in the category \mathsf{C}). Moreover, we’re placing a condition on R that does not mention \rho at all!
We therefore introduce the more refined (and more 2-categorical) concept of relatively initial functors. We show that these things satisfy some expected properties, such as forming a wide subcategory and being a proper generalisation of initial functors (“a functor is initial exactly when it is relatively initial with respect to the identity”). In fact, the relatively initial functors satisfy enough nice properties that we might be tempted to apply some homotopical-flavoured category theory here: can we localise the diagram category along the class of weak equivalences, using relatively initial functors as a calculus of fractions? The answer appears to be “yes”, but working out the details would have departed from the main path of the paper, which is already quite long. Hopefully, we will study them further in future work.
Finally, to step away from the category theory and back towards applications, we emphasize that the partial differential equations we have been talking about are largely independent of the underlying theory of diagrams, diagram morphisms, (extension-)lifting problems, and so on. Indeed, in the first blog post we actually talked about difference equations, which live in the setting of real vector spaces instead of sheaves on manifolds. Because of this, we hope to apply these techniques to other kinds of systems in the future, such as probabilistic and statistical models, particularly structural equation models.