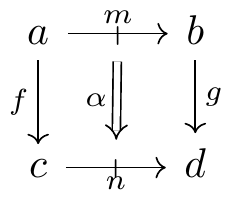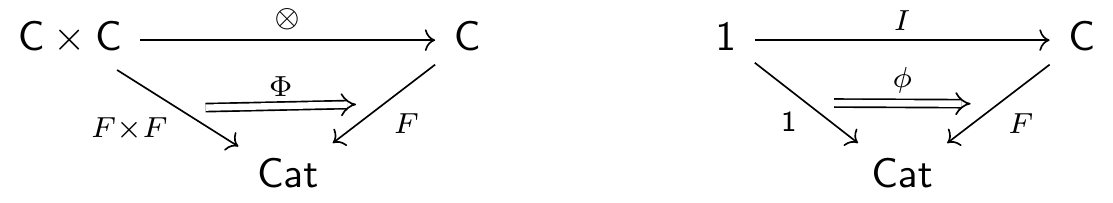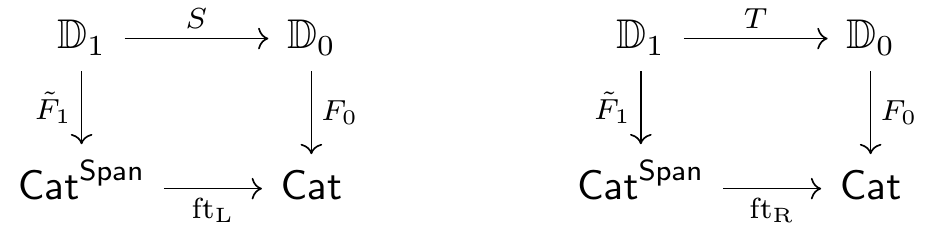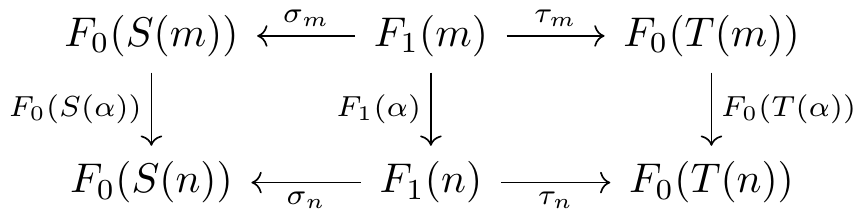Grothendieck construction for double categories
What is the Grothendieck construction for double categories? We explore one possible answer to this question, based on the perspective that double categories are categories internal to \mathsf{Cat}. In fact, we suggest a general procedure for doing the Grothendieck construction on any structure that is defined internally to \mathsf{Cat}.
Decorated cospans (Fong 2015), a tool for creating open systems out of closed ones, are now a mainstay of applied category theory and have been used in a range of contexts. In their refined form (Baez, Courser, and Vasilakopoulou 2022), decorated cospans form a double category and include structured cospans as a special case. Inasmuch as a decorated cospan consists of a cospan plus some extra stuff (the “decoration”), decorated cospans are analogous to objects in the Grothendieck construction. The latter are “decorated objects”: an object of a category plus some extra stuff. This suggests a puzzle: can the decorated cospan construction be reduced to a double-categorical version of the Grothendieck construction?
That would be nice, but what is the Grothendieck construction for double categories? Not much seems to be written about this. One source I know of is a talk (slides here) by Dorette Pronk (on joint work with Marzieh Bayeh and Martin Szyld) at the Topos Colloquium last year, in which a definition of the double Grothendieck construction is proposed. Here I will explore a different approach and try to derive a definition of the double Grothendieck construction. This leads to a different definition and right now I don’t understand how the two are related. Another definition of a double Grothendieck construction has been proposed by David Jaz Myers (Myers 2021), which the definition here turns out to generalize.
In this post, we’ll be preoccupied with thinking about the double Grothendieck construction. Next time I’ll show how this construction can recover decorated cospans and, more importantly, generalize them to interesting situations where the existing theory does not apply.
Update (01 June 2022): Geoffrey Cruttwell, Michael Lambert, Dorette Pronk, and Martin Szyld have just arXiv-ed a paper proposing a double Grothendieck construction equivalent to ours (Cruttwell et al. 2022, sec. 3.5). Moreover, unlike this blog post, they carefully treat the pseudo aspects of the theory and they prove a representation theorem that extends to double fibrations the classical equivalence between fibrations and category-valued pseudofunctors given by the Grothendieck construction. So check out their paper for a proper treatment of the double Grothendieck construction!
1 Structures internal to \mathsf{Cat}
Given a category \mathsf{C}, the data for the usual Grothendieck construction on \mathsf{C} is a functor F: \mathsf{C} \to \mathsf{Cat}. So, a first question is: given a double category \mathbb{D}, what is the input data for the Grothendieck construction on \mathbb{D}? Since the answer to this question doesn’t seem to be obvious, let’s try to answer a different one.
Suppose we want to define the data of the Grothendieck construction for some structure defined internally to \mathsf{Cat}. That is, we have an essentially algebraic theory \mathsf{T} (a.k.a., a finite limits theory) and we are considering the category of models of \mathsf{T} in \mathsf{Cat}, \mathsf{Mod}(\mathsf{T},\mathsf{Cat}) := \mathsf{Lex}(\mathsf{T},\mathsf{Cat}), whose objects are left exact functors M: \mathsf{T} \to \mathsf{Cat} (i.e., functors that preserve finite limits) and whose morphisms are natural transformations.
Here is an outline of an idea. Given a model M, we choose the decorations allowed for each category indexed by M by assigning, to each basic type (generating object) T of \mathsf{T}, a functor \bar{M}(T): M(T) \to \mathsf{Cat}. If we could suitably extend this assignment to the basic operations (generating morphisms) of \mathsf{T}, we would expect to obtain data \bar{M} from which we can build a new model by applying the standard Grothendieck construction pointwise. That is, we would obtain a model \int \bar{M}: \mathsf{T} \to \mathsf{Cat} such that (\int \bar{M})(T) = \int \bar{M}(T) for each basic type T.
The relevance of this speculation is that double categories are structures defined internally to \mathsf{Cat}; namely, they are categories internal to \mathsf{Cat}. Before proceeding further, let’s recall how that goes.
The theory of categories is an essentially algebraic theory \mathsf{T}_{\mathsf{Cat}} presented by
- objects \operatorname{Ob} and \operatorname{Hom};
- a pair of morphisms \operatorname{Hom}\rightrightarrows \operatorname{Ob}, for domain and codomain;
- morphisms \operatorname{Hom}\times_{\operatorname{Ob}} \operatorname{Hom}\to \operatorname{Hom} and \operatorname{Ob}\to \operatorname{Hom}, for composition and identities;
subject to the usual axioms. A (strict) double category is a model of the theory of categories in \mathsf{Cat}. Unpacking this definition in different notation, a double category \mathbb{D} consists of two categories \mathbb{D}_0 and \mathbb{D}_1 together with functors S,T: \mathbb{D}_1 \to \mathbb{D}_0 and \odot: \mathbb{D}_1 \times_{\mathbb{D}_0} \mathbb{D}_1 \to \mathbb{D}_1 \qquad\text{and}\qquad \operatorname{id}: \mathbb{D}_0 \to \mathbb{D}_1, subject to the category axioms. By convention (not shared by all authors), the objects of \mathbb{D}_0 are called the objects of the double category \mathbb{D}, the morphisms of \mathbb{D}_0 the arrows, the objects of \mathbb{D}_1 the proarrows, and the morphisms of \mathbb{D}_1 the cells. A cell \alpha: m \to n with S(\alpha) = f and T(\alpha) = g is depicted as the square:
The domain of the cell \alpha is m, the codomain is n, the source is f, and the target is g.
The most famous example of a structure internal to \mathsf{Cat} are monoidal categories; namely, a strict monoidal category is a model of the theory of monoids in \mathsf{Cat}. In this picture, a strict monoidal category consists of a category \mathsf{C} together with functors \otimes: \mathsf{C} \times \mathsf{C} \to \mathsf{C} and I: \mathsf{1} \to \mathsf{C} obeying the monoid axioms.
We expect that applying our generalized Grothendieck construction to the theory of monoids will recover the independently known Grothendieck construction for monoidal categories (Moeller and Vasilakopoulou 2020). Applying it to the theory of categories will yield a Grothendieck construction for double categories that decorates both objects and proarrows, in a compatible way.
Note: Our approach treats the two directions in a double category asymmetrically. At first glance that might seem odd, but it is consistent with recent works using pseudo double categories, in which the directions are inherently asymmetric: one is strict and the other is pseudo/weak. Indeed, the internalized definitions above are often too strict, and we need weak monoidal categories and pseudo double categories. However, to avoid extra complications, we will consider only the strict versions in this post.
2 Functorality of the Grothendieck construction
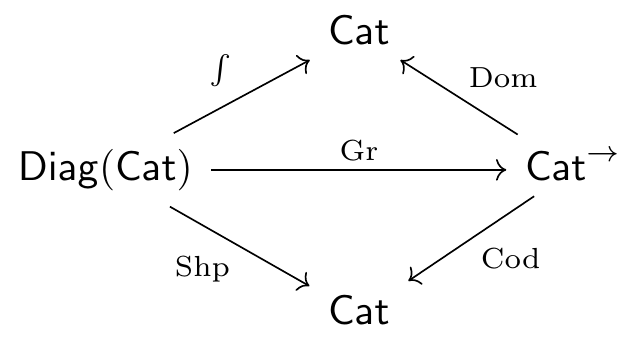
To complete the outlined construction, we need to get maps between the Grothendieck constructions that are taken pointwise. For this, we utilize the elegant result that the Grothendieck construction is functorial with respect to suitable morphisms. These morphisms are none other than morphisms of diagrams in \mathsf{Cat}. Diligent readers of the blog will recognize the concept of diagram morphisms from previous posts about categories of diagrams in physics.
Given a category \mathsf{C}, the diagram category \mathsf{Diag}(\mathsf{C}) has
- as objects, the diagrams in \mathsf{C}, which are functors F: \mathsf{J} \to \mathsf{C}, where \mathsf{J} is the shape of the diagram;
- as morphisms from F: \mathsf{J} \to \mathsf{C} to G: \mathsf{K} \to \mathsf{C}, the pairs (R,\rho) comprising a functor R: \mathsf{J} \to \mathsf{K} and a natural transformation \rho: F \Rightarrow G \circ R.
The category \mathsf{Diag}(\mathsf{C}) was denoted \mathsf{Diag}_{\rightarrow}(\mathsf{C}) in our previous posts and \mathsf{Diag}^\circ(\mathsf{C}) in (Peschke and Tholen 2020), which is our main reference for this section.
The shape functor \operatorname{Shp}:= \operatorname{Shp}^{\mathsf{C}}: \mathsf{Diag}(\mathsf{C}) \to \mathsf{Cat} sends a diagram to its shape and a diagram morphism (R,\rho) to R. When \mathsf{C} has finite limits, the category \mathsf{Diag}(\mathsf{C}) has finite limits too and the functor \operatorname{Shp}^{\mathsf{C}} preserves them (Peschke and Tholen 2020, Proposition 2.5, cf. Remark 2.8).
Now let’s consider diagrams in \mathsf{Cat}. The functorality of the Grothendieck construction is realized by the Grothendieck construction functor \operatorname{Gr}: \mathsf{Diag}(\mathsf{Cat}) \to {\mathsf{Cat}}^{\rightarrow} that sends
- a category-valued diagram F: \mathsf{J} \to \mathsf{Cat} to its Grothendieck construction along with the canonical projection: \pi_F: \int F \to \mathsf{J};
- a morphism of diagrams (R,\rho): (\mathsf{J}, F) \to (\mathsf{K},G) to the following commutative square, in which the functor \int (R,\rho) sends objects (j,x) to (Rj, \rho_j(x)) and morphisms (f,\phi): (j,x) \to (k,y) to (Rf, \rho_k(\phi)).
The relationships between the functors involved are summarized by the equations:
Note: In fact, Peschke and Tholen prove there is a 2-functor \operatorname{Gr}: \mathsf{CAT}/\mkern-6mu/\mathsf{Cat}\to {\mathsf{CAT}}^{\rightarrow}, where the 2-category \mathsf{CAT}/\mkern-6mu/\mathsf{Cat} has the same underlying 1-category as the 2-category \mathsf{DIAG}(\mathsf{Cat}) but has a richer 2-categorical structure (Peschke and Tholen 2020, Proposition 6.3). We are not going to worry about 2-categorical aspects or about distinguishing diagrams with small or large shapes.
What is important for us is that the functor \operatorname{Gr}: \mathsf{Diag}(\mathsf{Cat}) \to {\mathsf{Cat}}^{\rightarrow} is a right adjoint (Peschke and Tholen 2020, sec. 8) and hence preserves limits. Thus, the functor \int: \mathsf{Diag}(\mathsf{Cat}) \to \mathsf{Cat} also preserves limits.
Finally, it’s helpful to know that the functor \operatorname{Gr}: \mathsf{Diag}(\mathsf{Cat}) \to {\mathsf{Cat}}^{\rightarrow} is equivalently the natural transformation
with component \pi_F: \int F \to \mathsf{J} at diagram F: \mathsf{J} \to \mathsf{Cat}. This holds because, in general, a functor G: \mathsf{C} \to {\mathsf{D}}^{\rightarrow} is the same thing as a natural transformation (G \cdot \operatorname{Dom}) \Rightarrow(G \cdot \operatorname{Cod}): \mathsf{C} \to \mathsf{D}.
3 Grothendieck construction for structures in \mathsf{Cat}
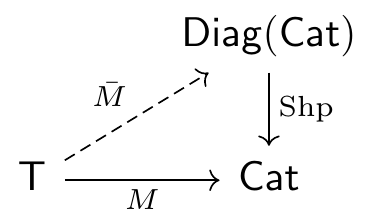
Given an essentially algebraic theory \mathsf{T}, data for the Grothendieck construction for \mathsf{Mod}(\mathsf{T},\mathsf{Cat}) is a model of \mathsf{T} in \mathsf{Diag}(\mathsf{Cat}). Alternatively, if we already have a model M: \mathsf{T} \to \mathsf{Cat} in mind, then data for a Grothendieck construction on M is a lift \bar M of M through the shape functor. The lift is in the category \mathsf{Lex}, meaning that \bar M must preserve finite limits.
We can now make the central definition of the post. Given an essentially algebraic theory \mathsf{T}, the Grothendieck construction of data \bar M: \mathsf{T} \to \mathsf{Diag}(\mathsf{Cat}) is:
Thus, we obtain a new model \int \bar{M} := \bar{M} \cdot \int together with a projection morphism of \int \bar{M} onto M = \bar{M} \cdot \operatorname{Shp}.
And that’s it! Once we’ve set everything up, the definition almost writes itself. But to understand what’s really going on, we need to unpack the construction for some particular choices of structure internal to \mathsf{Cat}. That requires a bit of honest work.
4 Monoidal Grothendieck construction
Let (\mathsf{C}, \otimes, I) be a strict monoidal category, which, we recall, is a monoid in \mathsf{Cat}. By the definition just given, Grothendieck data for \mathsf{C} consists of a functor F: \mathsf{C} \to \mathsf{Cat} together with natural transformations
having components \Phi_{a,b}: F(a) \times F(b) \to F(a \otimes b) for a,b \in \mathsf{C} and \phi_{*}: \mathsf{1} \to F(I), subject to the monoid axioms. This is precisely the data of a lax monoidal functor (F,\Phi,\phi): (\mathsf{C},\otimes,I) \to (\mathsf{Cat},\times,\mathsf{1}), with laxator \Phi and unitor \phi.
The Grothendieck construction of the data (F,\Phi,\phi) is a monoidal category with underlying category \int F. Its monoidal product is, on objects, (a,x) \otimes (b,y) = (a \otimes b, \Phi_{a,b}(x,y)), \qquad a,b \in \mathsf{M},\ x \in F(a),\ y \in F(b) and is (f,h) \otimes (g,k) = (f \otimes g, \Phi_{b,d}(h,k)) on morphisms (f: a \to b, h: Ff(x) \to y) and (g: c \to d, k: Fg(w) \to z), where we use the map F(f \otimes g)(\Phi_{a,c}(x,w)) = \Phi_{b,d}(Ff(x), Fg(w)) \xrightarrow{\Phi_{b,d}(h,k)} \Phi_{b,d}(y,z). Finally, the monoidal unit is (I, \phi_{*}(*)).
Apart from assuming that \mathsf{M} is strict and using a different variance convention, our construction agrees with the Grothendieck construction for monoidal categories (Moeller and Vasilakopoulou 2020, sec. A.1).
5 Double Grothendieck construction
We return at last to our main topic, the Grothendieck construction for double categories. It will take some work to unpack, and then re-pack, the definition.
According to our definition, Grothendieck data for a double category \mathbb{D} consists of two functors, F_0: \mathbb{D}_0 \to \mathsf{Cat} and F_1: \mathbb{D}_1 \to \mathsf{Cat}; two natural transformations
having components \sigma_m: F_1(m) \to F_0(S(m)) and \tau_m: F_1(m) \to F_0(T(m)) for each m \in \mathbb{D}_1; and two more natural transformations
having components \Gamma_{m,n}: (F_1 \times_{F_0} F_1)(m,n) \to F(m \odot n) for (m,n) \in \mathbb{D}_1 \times_{\mathbb{D}_0} \mathbb{D}_1 and \gamma_a: F_0(a) \to F_1(\operatorname{id}_a) for a \in \mathbb{D}_0, which all together satisfy the category axioms.
In the most complicated operation, composition, the category \mathbb{D}_1 \times_{\mathbb{D}_0} \mathbb{D}_1 is the pullback of \mathbb{D}_1 \xrightarrow{T} \mathbb{D}_0 \xleftarrow{S} \mathbb{D}_1. Less obviously, the functor F_1 \times_{F_0} F_1 is defined on objects (m,n) \in \mathbb{D}_1 \times_{\mathbb{D}_0} \mathbb{D}_1 by the pullback
in \mathsf{Cat}, and on morphisms by the universal property of the pullback. If you’re wondering where this came from: this is how you compute pullbacks in a diagram category.
Before going further, let’s pause to consider the interpretation of this data.
- The functors F_0: \mathbb{D}_0 \to \mathsf{Cat} and F_1: \mathbb{D}_1 \to \mathsf{Cat} assign categories of decorations to the objects and proarrows of \mathbb{D}.
- The transformations \sigma: F_1 \Rightarrow F_0 \circ S and \tau: F_1 \Rightarrow F_0 \circ T map decorations of proarrows to decorations of their source and target objects.
- The transformations \Gamma and \gamma define a composition law for decorations of proarrows with compatibly decorated source/target.
Now, if data for the usual Grothendieck construction is a functor into \mathsf{Cat}, and data for the monoidal Grothendieck construction is a lax monoidal functor into (\mathsf{Cat}, \times, \mathsf{1}), then is data for the double Grothendieck construction a lax double functor and, if so, into what?
Given a category \mathsf{C} with finite limits, recall that there is a (pseudo) double category of spans in \mathsf{C}, denoted \mathbb{S}\mathsf{pan}(\mathsf{C}), with
- objects, the objects of \mathsf{C}
- arrows, the morphisms of \mathsf{C}
- proarrows, spans in \mathsf{C}
- cells, commutative diagrams of form
Composition of proarrows is by pullback in \mathsf{C}.
As a structure internal to \mathsf{Cat}, the double category of spans in \mathsf{C} has \mathbb{S}\mathsf{pan}(\mathsf{C})_0 = \mathsf{C} and \mathbb{S}\mathsf{pan}(\mathsf{C})_1 = \mathsf{C}^\mathsf{Span}, where \mathsf{Span}:= \{\bullet \leftarrow \bullet \rightarrow \bullet\} is the walking span. Its source and target functors S,T are \operatorname{ft}_L, \operatorname{ft}_R: \mathsf{C}^\mathsf{Span}\to \mathsf{C}, extracting the left and right feet of a span. There is also a functor \operatorname{apex}: \mathsf{C}^\mathsf{Span}\to \mathsf{C} extracting the apex of a span.
Sketch of Proof. We have already unpacked the definition of Grothendieck data for \mathbb{D}. Let’s unpack the definition of the lax double functor and see that it’s the same thing. Consider a lax double functor (\tilde F, \tilde\Gamma, \tilde\gamma): \mathbb{D} \to \mathbb{S}\mathsf{pan}(\mathsf{Cat}). It consists, first of all, of functors F_0 := \tilde F_0: \mathbb{D}_0 \to \mathsf{Cat} and \tilde F_1: \mathbb{D}_1 \to \mathsf{Cat}^\mathsf{Span}. By the external functorality of the double functor \tilde F, we have commutative squares:
We can therefore define F_1: \mathbb{D}_1 \to \mathsf{Cat} on objects, as well as the components of the transformations \sigma: F_1 \to F_0 \circ S and \tau: F_1 \to F_0 \circ T, by the equation \tilde F_1(m) = \left\{ F_0(S(m)) \xleftarrow{\sigma_m} F_1(m) \xrightarrow{\tau_m} F_0(T(m)) \right\}, \qquad m \in \mathbb{D}_1. Similarly, we can define F_1: \mathbb{D}_1 \to \mathsf{Cat} on morphisms, and establish the naturality of \sigma and \tau, by equating \tilde F_1(\alpha) with
for every morphism \alpha: m \to n in \mathbb{D}_1. In other words, we have F_1 := \operatorname{apex}\circ \tilde F_1.
Finally, we can identify the laxator \tilde\Gamma, having components \tilde\Gamma_{m,n}: \tilde F_1(m) \odot \tilde F_1(n) \to \tilde F_1(m \odot n), \qquad m, n \in \mathbb{D}_1 \text{ with } T(m) = S(n), with the transformation \Gamma in the Grothendieck data, since the apex of the composite span \tilde F_1(m) \odot \tilde F_1(n) is (F_1 \times_{F_0} F_1)(m,n) and the apex of \tilde F_1(m \odot n) is F_1(m \odot n). Likewise, we can identify the unitor \tilde\gamma with the transformation \gamma. \square
So much for the data of the double Grothendieck construction. To conclude, let’s briefly describe the double category itself.
Given a lax double functor \tilde F: \mathbb{D} \to \mathbb{S}\mathsf{pan}(\mathsf{Cat}), identified with F: \mathsf{T}_{\mathsf{Cat}}\to \mathsf{Diag}(\mathsf{Cat}) as just explained, the Grothendieck construction on this data is, in the first place, a double category \int F with underlying categories (\int F)_0 = \int F_0 and (\int F)_1 = \int F_1. Explicitly, the double category \int F has
- objects, the pairs (a,x) with a \in \mathbb{D}_0 and x \in F_0(a)
- arrows (a,x) \to (b,y), the pairs (f,\phi) with f: a \to b in \mathbb{D}_0 and \phi: F_0 f(x) \to y in F_0(b)
- proarrows, the pairs (m,s) with m \in \mathbb{D}_1 and s \in F_1(m)
- cells (m,s) \to (n,t), the pairs (\alpha,\nu) with \alpha: m \to n in \mathbb{D}_1 and \nu: F_1 \alpha(s) \to t in F_1(n).
Next, sources and targets in \int F are defined by the functors \int (S,\sigma) and \int (T,\tau), which respectively send:
- proarrows (m,s) to (S(m), \sigma_m(s)) and (T(m), \tau_m(s))
- cells (\alpha,\nu): (m,s) \to (n,t) to (S(\alpha), \sigma_n(\nu)) and (T(\alpha), \tau_n(\nu)).
To summarize the situation so far, a generic cell in the double category \int F can be depicted as:
Finally, external composition in \int F is performed as follows.
- Composable proarrows (a,x) \xrightarrow{(m,s)} (b,y) \xrightarrow{(n,t)} (c,z) have composite (m \odot n, \Gamma_{m,n}(s,t))
- Cells (m,s) \xrightarrow{(\alpha,\nu)} (n,t) and (o,u) \xrightarrow{(\beta,\pi)} (p,v) that are composable, i.e., (T(\alpha), \tau_n(\nu)) = (S(\beta), \sigma_p(\pi)), have composite (\alpha \odot \beta, \Gamma_{n,p}(\nu,\pi))
- The identity proarrow at object (a,x) is (\operatorname{id}_a, \gamma_a(x))
- The identity cell at arrow (f, \phi): (a,x) \to (b,y) is (\operatorname{id}_f, \gamma_b(\phi))
Note: We don’t have to prove that \int F is a double category, nor that the canonical projection \pi_F: \int F \to \mathbb{D} with (\pi_F)_0 = \pi_{F_0}: \int F_0 \to \mathbb{D}_0 and (\pi_F)_1 = \pi_{F_1}: \int F_1 \to \mathbb{D}_1 is a double functor. That holds by construction!
Note: David Jaz Myers has introduced a double Grothendieck construction based on lax double functors into \mathbb{P}\mathsf{rof}, the pseudo double category of categories, functors, and profunctors (Myers 2021). A lax double functor into \mathbb{P}\mathsf{rof} can be turned into a lax double functor into \mathbb{S}\mathsf{pan}(\mathsf{Cat}) by post-composing with the double functor \mathbb{P}\mathsf{rof}\to \mathbb{S}\mathsf{pan}(\mathsf{Cat}) that sends a profunctor to its corresponding two-sided discrete fibration. The double Grothendieck construction here is then seen to generalize the one in (Myers 2021). Thanks to Brandon Shapiro for pointing this out.
6 Discussion
In a sequel post, we’ll use the Grothendieck construction for double categories to reconstruct and generalize decorated cospans.
When working with open systems, we usually want not just a double category but a monoidal double category. A fully strict monoidal double category is a double category \mathbb{D} where both \mathbb{D}_0 and \mathbb{D}_1 are equipped with the structure of monoids in \mathsf{Cat}, such that all the double category operations are monoid homomorphisms. These belong to the category \mathsf{Mod}(\mathsf{T}_{\mathsf{Cat}}, \mathsf{Mod}(\mathsf{T}_{\mathsf{Mon}}, \mathsf{Cat})). But, using the tensor product of essentially algebraic theories, this category is equivalent to \mathsf{Mod}(\mathsf{T}_{\mathsf{Cat}}\otimes \mathsf{T}_{\mathsf{Mon}}, \mathsf{Cat}). Thus, we could apply Grothendieck construction to the theory \mathsf{T}_{\mathsf{Cat}}\otimes \mathsf{T}_{\mathsf{Mon}} to obtain a Grothendieck construction for monoidal double categories. Unpacking that would take some effort. Still, it’s encouraging to know that, even for this properly three-dimensional categorical structure, there is a plausible procedure by which to derive its Grothendieck construction.
To do apply the Grothendieck construction to decorated cospans without resorting to strictification, we need pseudo double categories, specifically the pseudo double category of cospans. It seems that everything in this blog post extends from the 1-categorical to the 2-categorical level: a pseudo double category is a model in the 2-category \mathsf{Cat} of the finite limit 2-theory of a pseudo-category (Martins-Ferreira 2006), and the Grothendieck construction is a 2-functor \operatorname{Gr}: \mathsf{CAT}/\mkern-6mu/\mathsf{Cat}\to {\mathsf{CAT}}^{\rightarrow} and even the right part of a 2-adjunction (Peschke and Tholen 2020, sec. 8). Since all the elements needed are essentially known, working out this 2-categorical extension should in principle be straightforward—but it will take a better 2-category theorist than me to do it.