All models are wrong, but…
What makes a good mathematical model? For recent work at Topos, it’s when the model helps people cooperate to achieve collective goals. This has a few implications for how we design modelling software.
“All models are wrong, but some are useful” — George Box1
What is the purpose of a mathematical model? The above, well-known quote comes from a paper of statistician George Box, who makes the point that models never completely predict reality. As an example, he takes the ideal gas law, relating the pressure, volume, and temperature of a gaseous body. This ‘law’, he argues, is only a statistical approximation, and in fact reality diverges in a variety of subtle ways. Nonetheless, it is useful — it’s a close enough approximation that we can use it for precision engineering. It helps us make espresso machines and surgical equipment and space shuttles! In this view, while no model is perfect, a good model is one that extrapolates well to new data.
In collaboration with teams led by epidemiologist and public health expert Professor Nate Osgood and computer scientist James Fairbanks, Topos scientists Evan Patterson, Sophie Libkind, and John Baez recently published two papers on rapid epidemic modelling. They’re really lovely papers, backed by software and simulations, which use compositional ideas from category theory to show how models can be rapidly constructed from high level descriptions. Assisted by additional discussions with Nate, Evan, and Sophie, this paper has highlighted what is for me a new perspective on mathematical modelling, and one I believe very much reflects the spirit of our mission at Topos. In their view, a good mathematical model is one that helps diverse parties agree on the likely future consequences of their actions.
To dive straight into the papers, check them out here:
- Compositional Modeling with Stock and Flow Diagrams. John Baez, Xiaoyan Li, Sophie Libkind, Nathaniel Osgood, and Evan Patterson. arXiv:2205.08373
- An Algebraic Framework for Structured Epidemic Modeling. Sophie Libkind, Andrew Baas, Micah Halter, Evan Patterson, and James Fairbanks. arXiv:2203.16345
Mathematical modelling has played a central, public role in the COVID-19 pandemic. Especially in the uncertainty of the early pandemic, mathematical models were one way to access a bit more information about the possible future. How many deaths will COVID cause? When will this wave end? When can life get back to ‘normal’? Yet these models are unlike our ideal gas law in a key sense: these questions were (and continue to be) dependent on our behaviour as individuals and as a society. When a pandemic model predicts an unacceptable burden of death and disease, we have the power to make it ‘wrong’, to avert this potential future becoming our reality. In this case, a model might be excellent precisely because its predictions completely diverge from future reality — the excellence lies in the fact that the model galvanizes changes in policy and behaviour to save lives.
That is: a model can be excellent because it becomes wrong!
This different view of “what is a good model” implies different goals for good modelling methodology. For example, models that predict complex phenomena precisely are often necessarily themselves complex. On the other hand, complexity makes models harder to understand, and therefore less accessible to those without a vast amount of technical experience. Nonetheless, it’s important that such people, which can include influential decision makers, let alone the wider public, feel comfortable trusting models that they use to make decisions. Without this trust, it’s harder to find agreement, and cooperate towards a future everyone believes in. Thus a good modelling methodology must consider the balance between precision and transparency.
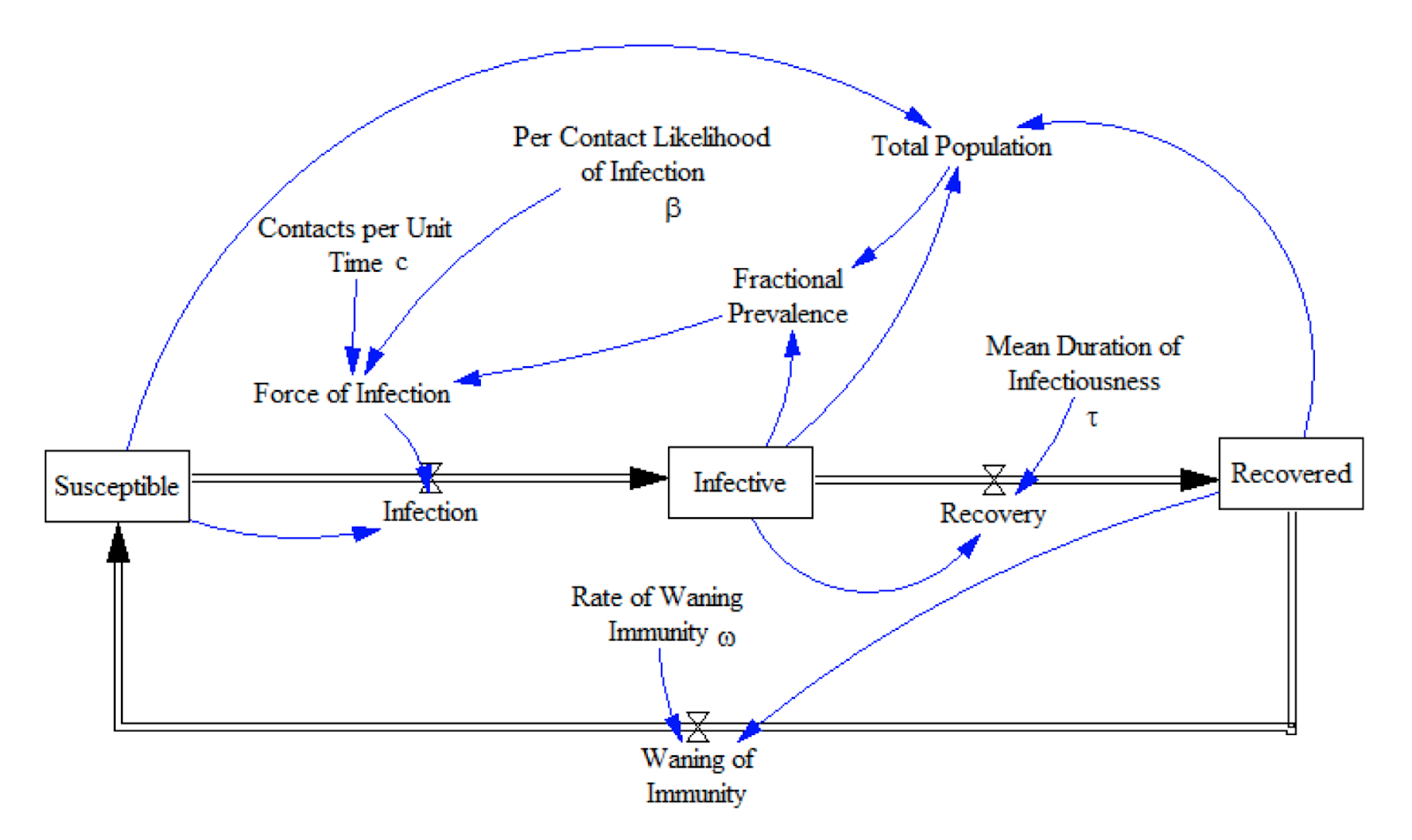
In these papers, the authors develop a number of techniques to increase transparency of models. First, they use high level models, in terms of descriptions of concepts people can relate to, such as susceptible and infective populations and encounters between them, rather than using anonymous variables like ‘p’ and ‘q’ that change according to a differential equation.
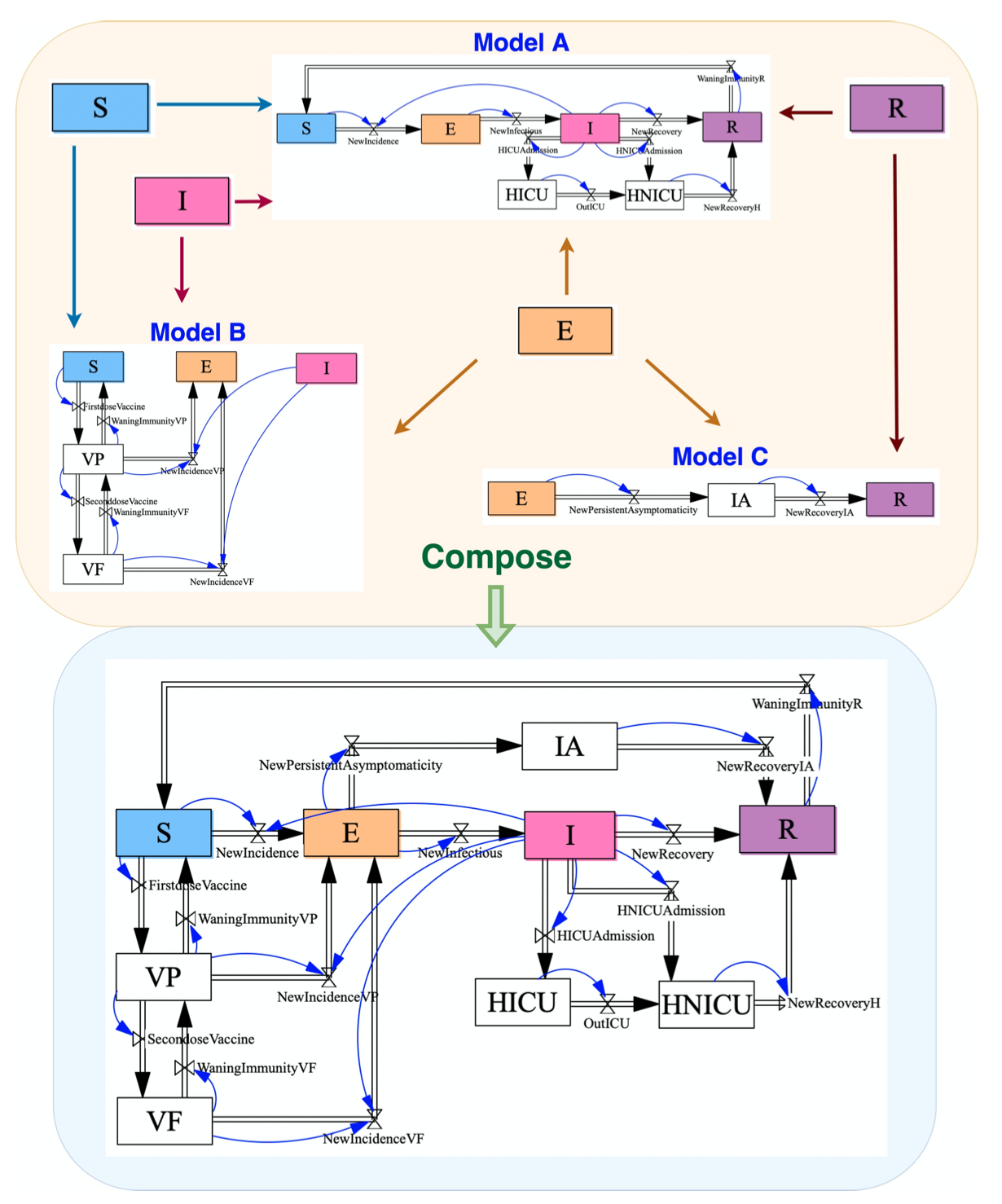
Second, they use visual models. This increases accessibility of the models, giving all parties a sense of what they mean without requiring the ability to, for example, read and interpret differential equations. This is especially important when various stakeholders in the decision-making process, like public policy makers, or even the general public, have not necessarily had years of formal training in mathematical modelling. Note that in this case the diagrams have formal meaning: the diagrams are not merely depictions of a mathematical model, they are themselves the model!
Third, they emphasise the compositionality of models: building up models from simpler parts. Complex phenomena like pandemics involve many distinct parts. The expertise to understand each part is often held by a different person: epidemiologists, geneticists, economists, behavioural psychologists, and politicians may each hold a distinct piece of the puzzle. Compositional modelling allows each expert to create and verify a model representing their insights into the situation, while having that model feed directly and robustly into the large scale vision. This further increases the chance that the model reliably reflects what each expert thinks, and increases buy-in and trust from each party.
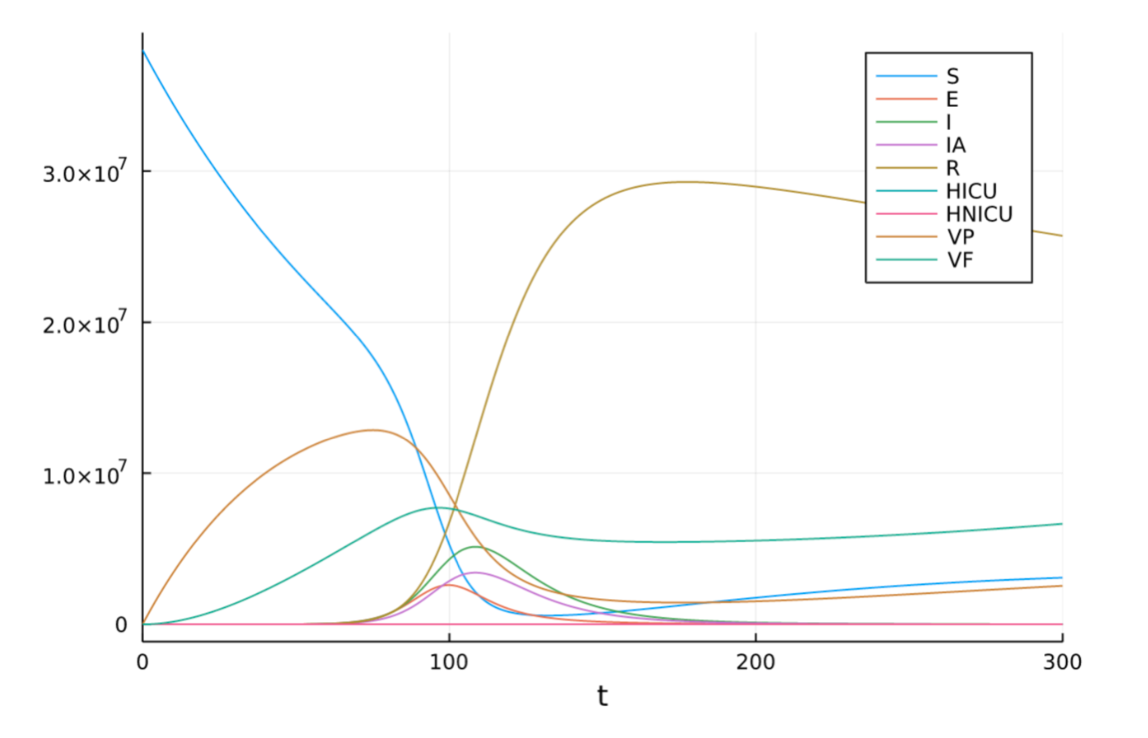
All in all, these features of transparent model construction mean that when the models ultimately print out predictions about the future, it is clearer what assumptions led to these predictions, and hence what options we have, as a society, if we want to secure or avoid such a future.
While a definition of excellence in modelling that just makes reference to data is technically neat and does provide an important measure of quality, at Topos the end goal of our work is always to improve the lives of people. This means that ultimately we believe we must tie the quality of our mathematics and our programming tools to how people interact with it. In this case, our work is successful when it helps people agree, so they can more fully cooperate, and make collective decisions with outcomes that better reflect their hopes and values.
Footnotes
Box, G. E. P. (1979), “Robustness in the strategy of scientific model building”, in Launer, R. L.; Wilkinson, G. N. (eds.), Robustness in Statistics, Academic Press, pp. 201–236, doi:10.101/B978-0-12-438150-6.50018-2, ISBN 9781483263366.↩︎