Promonoidal categories and wiring diagrams
There are (colored) operads for all sorts of different flavors of wiring diagrams: those governing monoidal categories, symmetric monoidal categories, traced categories, compact closed categories, hypergraph categories, etc. But all of these operads are in fact more than mere operads: there’s a sense in which you can take any operation, cluster together various objects in it, and thereby factor the operation. Operads are about how operations compose, but we seem to be able to factor, or decompose operations. What gives? At a recent workshop, Mario Román explained pro-monoidal categories to me, and he conjectured that wiring diagram operads are pro-monoidal; I agree and, though I haven’t proven it, I’ll present the conjectural idea below.
1 Introduction
Recently, Topos Institute hosted a workshop called Finding the right abstractions for healthy systems. It brought together 24 researchers, about half of whom are applied category theorists and the other half of whom are mathematicians, philosophers, physicists, etc., mainly from the AI safety community. We spent a week discussing how to think about health, e.g. in terms of sense-making, boundaries, and categorical systems theory.
The event followed one we had during the pandemic, in May 2020, called Finding the right abstractions for human flourishing. I much prefer the in-person format, which focused not on outputs but on collaboration and learning.
In this post I want to just write about one thing I learned from the week: how to think about pro-monoidal categories. I’d seen these before: just like a monoidal category consists of a category \mathcal{C} and functors \mathbf{1}\to\mathcal{C} \qquad\text{and}\qquad \mathcal{C}\times\mathcal{C}\to\mathcal{C} satisfying unitality and associativity, a promonoidal category consists of a category \mathcal{C} and profunctors \mathbf{1}\nrightarrow\mathcal{C} \qquad\text{and}\qquad \mathcal{C}\times\mathcal{C}\nrightarrow\mathcal{C} satisfying unitality and associativity. But how are you supposed to think about all this data? I didn’t have the motivation to really work on it before, so I thought I’d wait until the day that someone could explain it to me and why I should care. Luckily that day came at the FRA workshop, when Mario Román explained the idea to me. He conjectured that wiring diagram operads are in fact pro-monoidal, and I found this idea very interesting.
There are (colored) operads for all sorts of different flavors of wiring diagrams: those governing monoidal categories, symmetric monoidal categories, traced categories, compact closed categories, hypergraph categories, etc. But all of these operads are in fact more than mere operads: there’s a sense in which you can take any operation, cluster together various objects in it, and thereby factor the operation.
Operads are about how operations compose, but we seem to be able to factor, or decompose operations. What gives? As Mario explained to me, this is what pro-monoidality gives you. I’ll explain the idea below.
2 How to think about promonoidal categories
How are we supposed to think about the profunctors \mathbf{1}\nrightarrow\mathcal{C} and \mathcal{C}\times\mathcal{C}\nrightarrow\mathcal{C}? That is, how should we think about functors \mathcal{O}_0\colon\mathcal{C}\to\mathbf{Set} \qquad\text{and}\qquad \mathcal{O}_2\colon(\mathcal{C}\times\mathcal{C})^\textnormal{op}\times\mathcal{C}\to\mathbf{Set} The idea Mario explained to me is that we should think of the morphisms in \mathcal{C} as 1-ary operations, and that the profunctors \mathcal{O}_0 and \mathcal{O}_2 are telling us about 0-ary and 2-ary operations on \mathcal{C}.
Let’s start with \mathcal{O}_2. If you have objects c_1,c_2,d\in\mathcal{C}, then you have a set \mathcal{O}_2((c_1,c_2),d):\mathbf{Set} We should think of this set as that of all 2-ary operations with input types (c_1,c_2) and output type d. For example, if there is an element \varphi\in\mathcal{O}_2((c_1,c_2),d), we would denote it in a bubble (read left-to-right) like so:
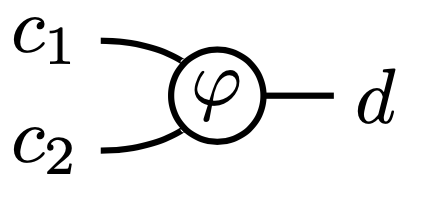
The fact that \mathcal{O}_2 is a profunctor means that we can act on such a \varphi using maps f_1\colon c_1'\to c_1 and f_2\colon c_2'\to c_2 in \mathcal{C}^\textnormal{op} and g\colon d\to d' in \mathcal{C}. The above situation is drawn in the “obvious way”

The point is that the profunctor makes this composite thing into a well-defined element of \mathcal{O}_2((c_1',c_2'),d').
Similarly, elements \psi\in \mathcal{O}_0(d) are drawn as 0-ary operations
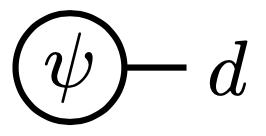
The unitality condition says that the profunctor you get by composing \mathcal{O}_2 and \mathcal{O}_0 is the hom-profuctor \mathcal{C}\nrightarrow\mathcal{C}, i.e. \mathcal{C}(-,-)\colon \mathcal{C}^\textnormal{op}\times\mathcal{C}\to\mathbf{Set}. In other words the set of all possible composites of 0-ary operations and 2-ary operations

after quotienting out the “unexposed” morphisms x\to x' in \mathcal{C}, is precisely the set of morphisms c\to d in \mathcal{C}. Not only can you compose any 0-ary and 2-ary morphism to get a 1-ary morphism, but every 1-ary morphism factors as a composite of 0-ary and 2-ary morphisms. And of course this holds for the other unitality condition as well
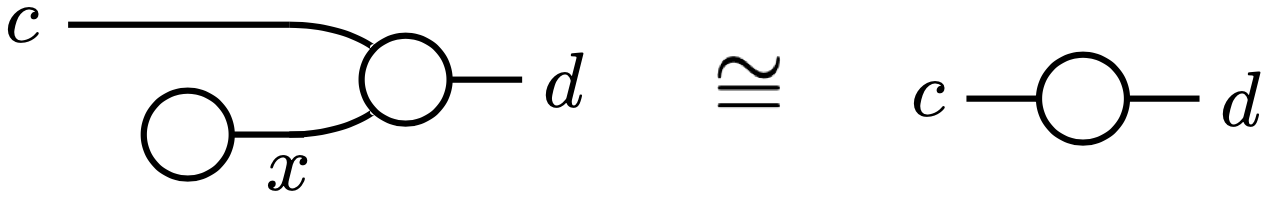
The associativity condition says that the two profunctors \mathcal{C}\times\mathcal{C}\times\mathcal{C}\nrightarrow\mathcal{C} one obtains by composing \mathcal{O}_2 with itself on one string or the other are the same

Again, this means the set of all ways to compose as on the left is in bijection with the set of all ways to compose as on the right, modulo 1-ary morphisms on the strings labeled x and x'.
Thus we can think of a pro-monoidal category as a (colored) operad whose operations are composites of 0-ary and 2-ary morphisms, with some added conditions given by the unitality and associativity isomorphisms as discussed above. Brandon Shapiro is quick to point out that this notion is not actually biased to 0-ary and 2-ary operations; it just appears that way from this point of view. He conjectures that you can identify a promonoidal category with an operad that has been equipped with a Conduché fibration to the terminal operad. This is a beautiful idea: it means that for any n-ary operation \varphi and tree t with n-many leaves, there is a non-empty and connected category whose objects are t-factorizations of \varphi. But we will not explore this here.
3 Background on wiring diagram operads
There are (colored) operads governing all sorts of different kinds of categories. For example, Dylan Rupel, Patrick Schultz, and I showed that the operad governing traced monoidal props is 1-\mathbf{Cob}, i.e. that the category of traced monoidal props is the category of algebras for this operad. Similarly, Brendan Fong and I showed showed that the category of hypergraph props is that of algebras for the operad \mathbf{Cospan}_\mathbf{Fin}, and Evan Patterson, Dmitry Vagner, and I gave an operad whose algebras are symmetric monoidal props. As explained in the papers linked above, the story for traced, compact, hypergraph, and monoidal categories (rather than props) is just a matter of adding string labels to these operads.
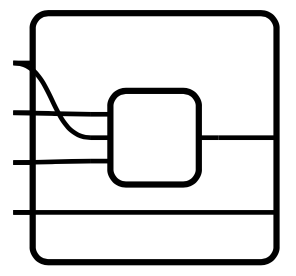
The idea is that for every kind of category, call them X-categories—here X might be vanilla, monoidal, cartesian monoidal, traced monoidal, hypergraph, etc.—there is a kind of string diagram that governs how its morphisms can compose. If you think of each morphism as inhabiting a box-with-ports

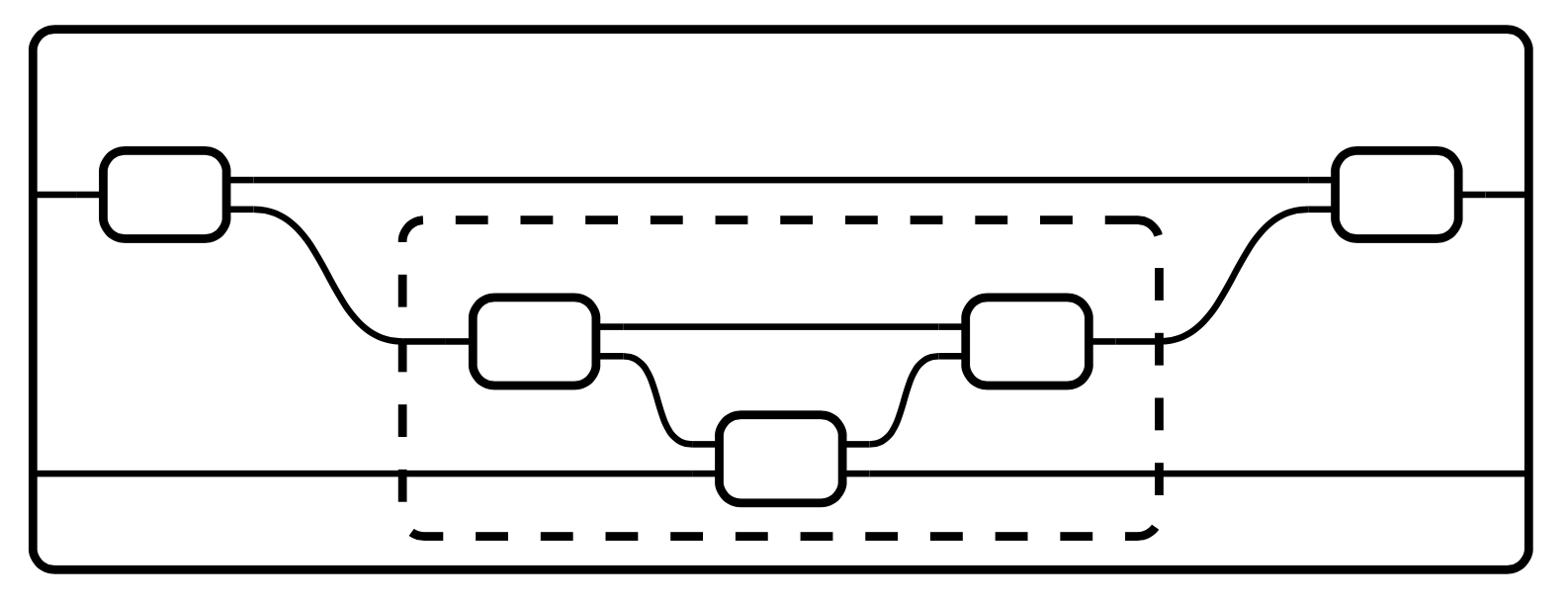
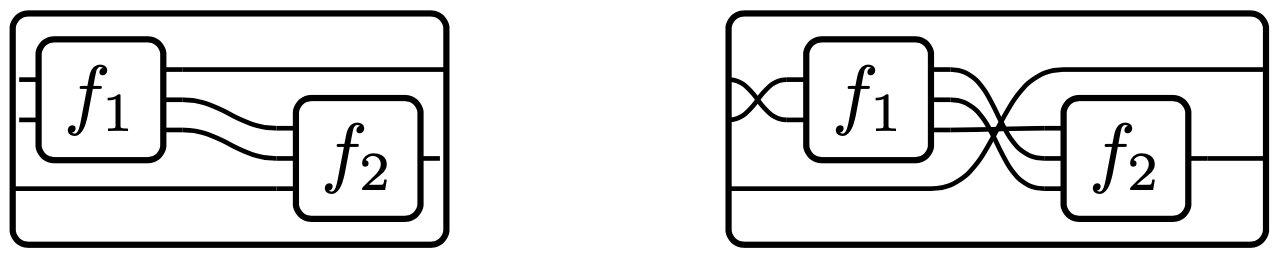
then X-categories have a notion of legal arrangements for putting little boxes inside a big box, e.g. here is an arrangement that’s legal in traced monoidal categories:
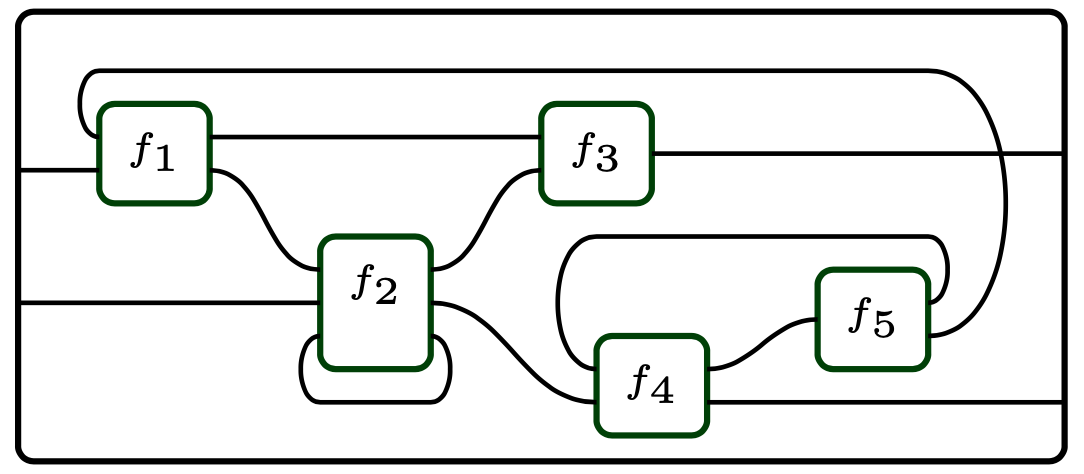
We can thus say that the operad has “boxes with ports” as its objects (colors), and it has the above sort of “legal arrangements” as its operations. Composition in the operad corresponds to nesting boxes within boxes in the above sorts of wiring diagram pictures.
Now out of all the operads we’ve used to describe various sorts of categories, almost all of them (e.g. 1-\mathbf{Cob} and \mathbf{Cospan}_\mathbf{Fin}) are in fact representable operads, meaning that they underlie monoidal categories. This means that any such wiring diagram can be written by first stacking all the interior boxes in a “trench coat”
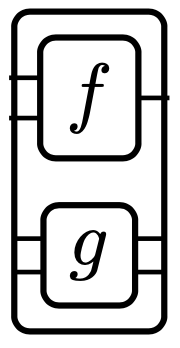
and then do all of the wiring from there.
However, the operads governing monoidal categories and symmetric monoidal categories are not representable. The reason is that morphisms in a monoidal category need to progress in order; there is no feedback allowed.
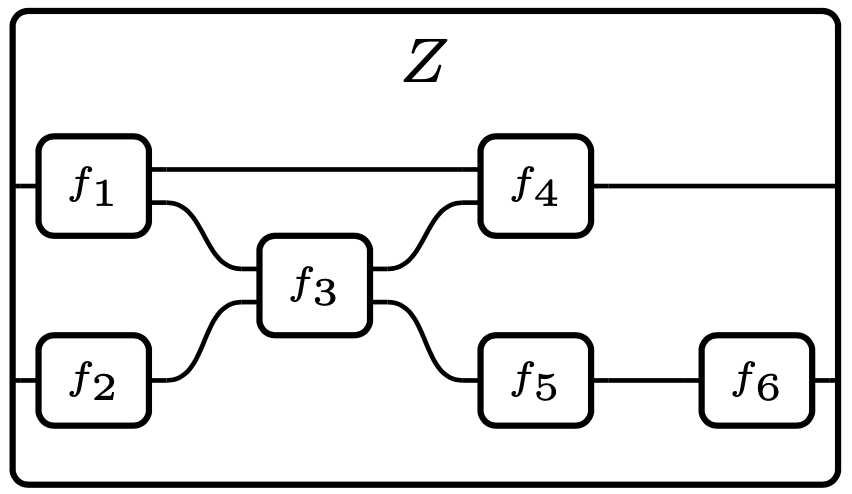
This “ordered progress” condition simply cannot be stated if you were to stack f_1,\ldots,f_6 together in a trenchcoat before writing down the wiring.
However, even though the operads for monoidal and symmetric monoidal categories are not representable, they are more than mere operads. You can cluster arbitrary boxes (including the wiring between them) as long as you don’t skip any intermediary boxes.
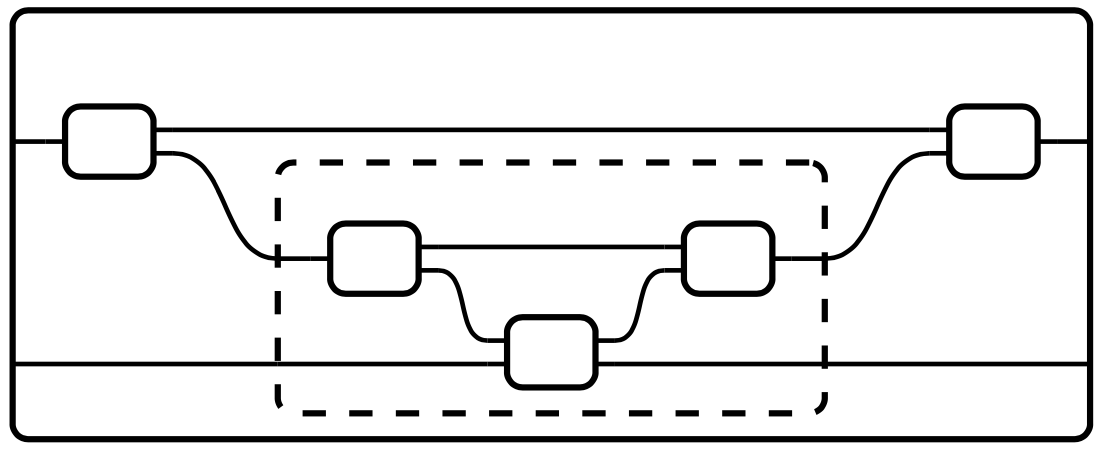
The fact that you can compose the stuff inside the dotted box with the stuff outside the dotted box is captured by the definition of operad. But the fact that you can decompose by clustering is not captured by the definition of operad. This is a common point of confusion, for which I did not previously have any story.
Luckily, Mario’s explanation of pro-monoidal categories explains where this clustering ability comes from. As we saw before, pro-monoidal categories are like operads, except that every n-ary morphism can be decomposed.
We should note that any monoidal category is pro-monoidal, because functors 1\to\mathcal{C} and \mathcal{C}\times\mathcal{C}\to\mathcal{C} are special profunctors. So the clustering ability that pro-monoidal categories give us was already there for many of the wiring diagram operads we use. Again, the exceptions we know of are monoidal and symmetric monoidal categories. We’ll end this post by explaining the pro-monoidal category for symmetric monoidal categories.
4 The pro-monoidal category governing symmetric monoidal categories
A prop is a symmetric monoidal category whose objects are in bijection with \mathbb{N} and for which the monoidal structure is (0,+). You can think of n\in\mathbb{N} as a number of strings. A colored prop allows you to have different labels on strings: its objects are \mathrm{List}(C) where C is a set (with elements called “colors”). Every symmetric monoidal category is equivalent to a colored prop, so it suffices to work with colored props. For simplicity we will only work with one-colored props, but it should be fairly straightforward for an interested reader to extend the ideas to have colored strings.
In an arbitrary prop, what is the set of legal ways to arrange morphisms f_1 and f_2 to form a morphism g? And what if you didn’t have access to any morphisms; what morphisms h could you build for free? The answers to these two questions should be the sets \mathcal{O}_2((f_1,f_2),g) \qquad\text{and}\qquad \mathcal{O}_0(h) where \mathcal{O} is the promonoidal category governing props. So what are \mathcal{O}_2 and \mathcal{O}_0? We’ll give the full definition below, but let’s start with examples.
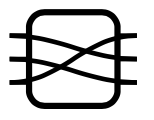
If f_1\colon 2\to 3 and f_2\colon 3\to 1 and g\colon 3\to 2, then here are two possible wirings of f_1 and f_2 in g:
If h\colon 3\to 3 then the set \mathcal{O}_0(h) should contain 3!=6 elements, one of which is shown here:
So the idea is that our profunctors \mathcal{O}_2 and \mathcal{O}_0 are telling us about all the ways to arrange two boxes, or zero boxes, within a box. It’s time to define them formally!
We will define the object set of \mathcal{C} to be the set \mathop{\mathrm{Ob}}(\mathcal{C})\coloneqq\mathbb{N}\times\mathbb{N}. The idea is that (n,n')\in\mathop{\mathrm{Ob}}(\mathcal{C}) is a box with n-many inputs and n'-many outputs. The hom-set \mathcal{C}((n,n'),(p,p')) is given by \{(f_1\colon p\to n+p', f_2\colon n'\to p')\mid (f_1,f_2)\colon p+n'\to n+p'\text{ is a bijection}\} These are all the ways to put the “n” box into the “p” box: a function p\to n+p' says for every input to the outer box, choose either an input to the inner box or an output of the outer box; a function n'\to p' says for every output of the inner box, choose an output of the outer box; the bijection condition says to make sure everything is hit exactly once. For example, here is an element of \mathcal{C}((3,1),(4,2)):
The profunctor \mathcal{O}_0\colon\mathbf{1}\nrightarrow\mathcal{C}, i.e. the functor \mathcal{O}_0\colon\mathcal{C}\to\mathbf{Set} sends (n,n') to the set of all bijections n\cong n', which is empty if n\neq n' and has n!-many elements if n=n'.
The profunctor \mathcal{O}_2\colon\mathcal{C}\times\mathcal{C}\nrightarrow\mathcal{C} applied to ((n_1,n_1'),(n_2,n_2');(p,p')) is the set \left\{ \left( \begin{aligned} f_1&\colon p\to n_1+n_2+p', \\f_2&\colon n_1'\to n_2+p', \\f_3&\colon n_2'\to p' \end{aligned} \right) \;\middle|\; p+n_1'+n_2'\xrightarrow{(f_1,f_2,f_3)} n_1+n_2+p'\text{ is a bijection} \right\} We will not show that these satisfy associativity and unitality, nor that monoidal props are exactly the \mathcal{O}-algebras (lax functors \mathcal{O}\to\mathbf{Set}); anyone who does so can take all the credit for themselves, except whatever they owe Mario for thinking of this idea and whatever they owe me for explaining it here :)
Let us know in the comments below if you come up with any other pro-monoidal categories of your own!