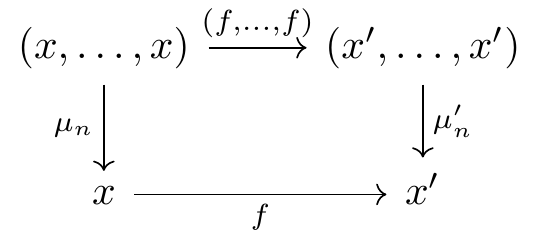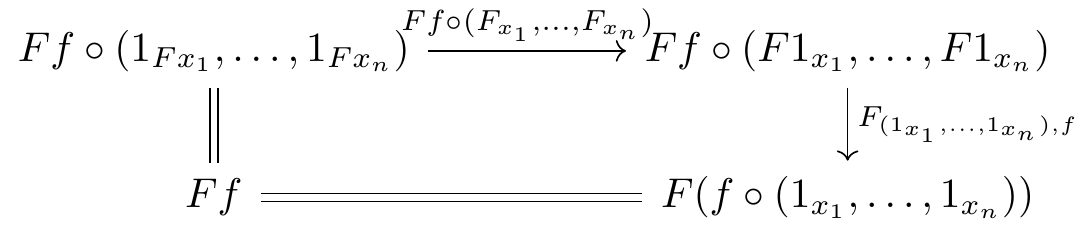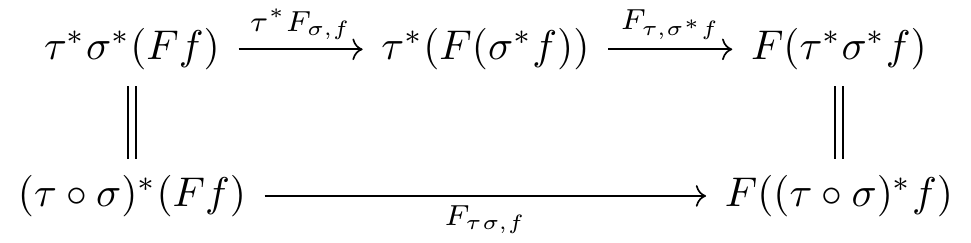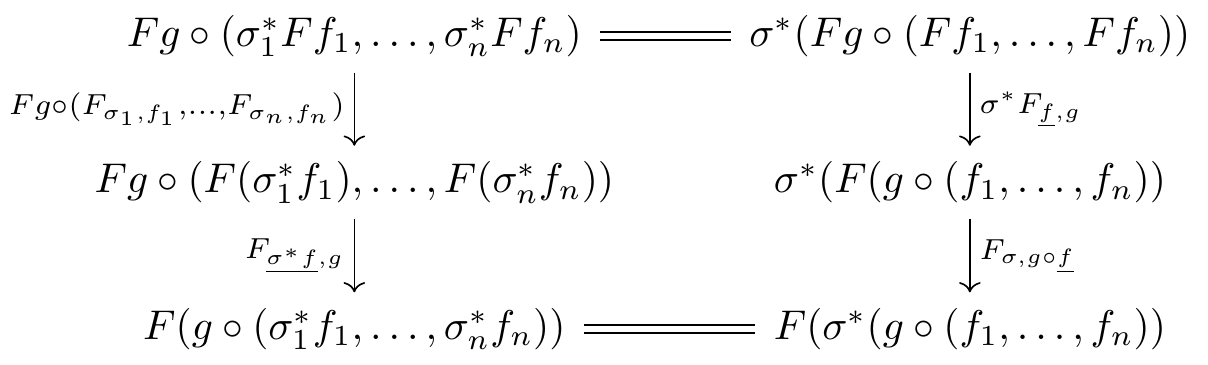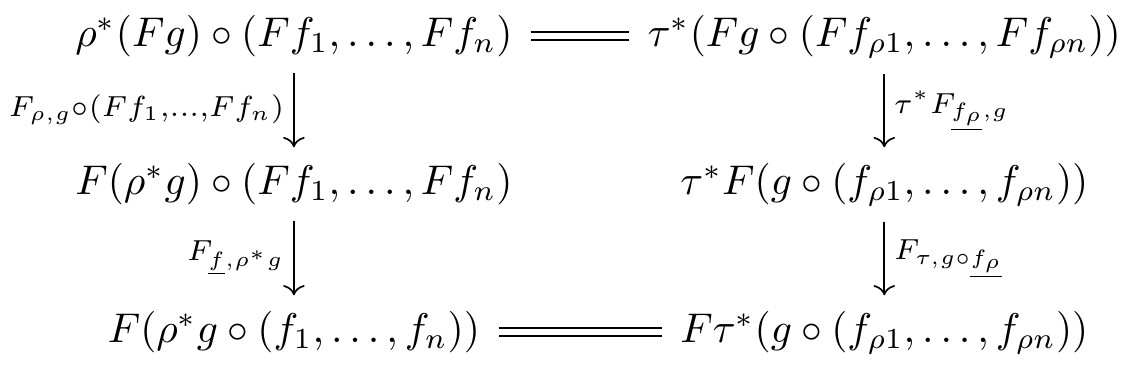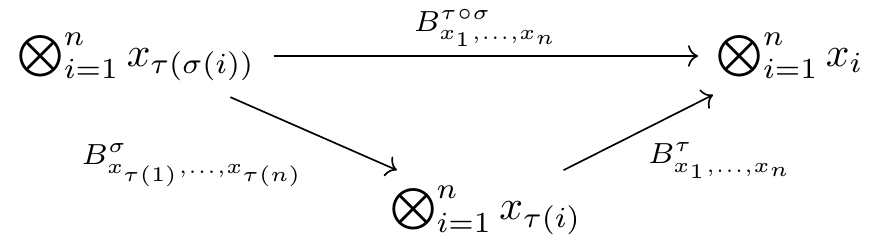Unbiased monoidal categories are pseudo-elements
Categorifying the observation that monoids are generalized elements of multicategories, we show that unbiased pseudomonoids, such as unbiased monoidal categories, are “pseudo-elements” of 2-multicategories.
Given that they are among the most commonplace concepts of category theory, monoidal categories are strangely unsatisfactory in some ways. In (weak) monoidal categories like those of sets or vector spaces, the associativity and unitality laws of a monoid hold only up to natural isomorphism, and the “associators” and “unitors” giving the natural isomorphisms need to obey certain coherence axioms. All that seems to be inevitable, but the particular selection of coherence axioms, known as Mac Lane’s pentagon and triangle identites, are rather mysterious at first sight. Why these axioms and not others?1
The definition of a monoidal category is justified by Mac Lane’s famous coherence theorem, which roughly states that once the pentagon and triangles commute, every “formal” diagram made out of associators and unitors commutes. Neither the precise statement nor the proof of this theorem is simple (Mac Lane 1998, chap. XI). Coherence for symmetric or braided monoidal categories presents further subtleties. In the epilogue to her category theory textbook, Riehl cites the coherence theorem for symmetric monoidal categories as an early example of a difficult theorem in category theory (Riehl 2016).
While the importance of the coherence theorem is undeniable, I have to admit that I prefer the simple theorems in category theory. The hard, yet mostly invisible, work should be in formulating the concepts; with the right ones, the proofs should follow with a minimum of effort. I take this to be part of what is meant in saying that category theory is “conceptual mathematics.”
Now, there is a conceptual way to define a monoidal category, but it requires taking the unbiased view. Algebraic structures such as monoids and categories are traditionally defined by postulating operations of certain arities, often binary operations and nullary operations (constants), and then generating operations of arbitrary arity from composites of these. Such definitions are “biased” in privileging certain arities over others. In the unbiased approach, one directly postulates operations of every arity and then adds axioms making all the operations be compatible with each other. Though not as well appreciated as they should be, notions of unbiased monoidal category can be found in literature (Deligne and Milne 1982; Leinster 2004, sec. 3.1). In unpublished notes, Brandenburg has proved that unbiased symmetric monoidal categories are equivalent to the usual ones (Brandenburg 2016).
In this post, we take this line of thinking one step further by showing that unbiased monoidal categories need not even be regarded as a primitive concept but can, without circularity, be derived from more basic ones. I would be surprised if no one has noticed this before, although I cannot find it in the literature. In any case, I think it’s a story that’s worth telling.
1 Monoids in multicategories
As a warm-up, let’s review how the concept of a monoid is implicit in the concept of a multicategory (Leinster 2004, Example 2.1.11).
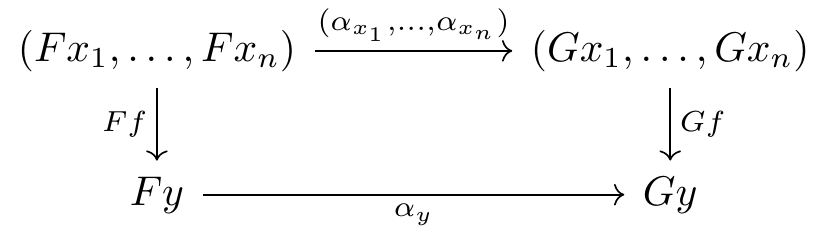
We first recall the main definitions concerning multicategories. A multicategory \mathcal{M} consists of a set of objects x, y, \ldots \in \mathcal{M} and, for every arity n \geq 0, families of n-ary multimorphisms \mathcal{M}(x_1, \dots, x_n; y), \qquad x_1, \dots, x_n, y \in \mathcal{M} whose elements are denoted f: (x_1,\dots,x_n) \to y. These are accompanied by composition operations \mathcal{M}(y_1,\dots,y_k; z) \times \prod_{i=1}^k \mathcal{M}(x_{i,1},\dots,x_{i,n_i}; y_i) \xrightarrow{\circ} \mathcal{M}(x_{1,1},\dots,x_{k,n_k}; z), \tag{1} whose action on multimorphisms g and f_1,\dots,f_k is denoted g \circ (f_1,\dots,f_k), and identity morphisms 1_x: x \to x for x \in \mathcal{M}, subject to laws of associativity and unitality. A multifunctor, or just a functor for short, between multicategories is the evident structure-preserving map: it sends objects to objects and n-ary multimorphisms to n-ary multimorphisms such that domains, codomains, composition, and identities are preserved. Finally, a natural transformation \alpha: F \Rightarrow G between multifunctors F, G: \mathcal{M} \to \mathcal{N} consists of a unary2 morphism \alpha_x: Fx \to Gx in \mathcal{N} for every object x \in \mathcal{M}, such that for every multimorphism f: (x_1, \dots, x_n) \to y in \mathcal{M}, the naturality square
commutes. Multicategories, multifunctors, and natural transformations form a 2-category \mathbf{Mlt} (Hermida 2000, sec. 6).
The standard biased definition of a monoid makes sense in any multicategory. A monoid in a multicategory \mathcal{M} consists of an object x \in \mathcal{M}, the carrier, along with a binary morphism \mu: (x,x) \to x and a nullary morphism \eta: () \to x, the multiplication and the unit, satisfying the usual associativity and unitality laws. A monoid homomorphism (x,\mu,\eta) \to (x',\mu',\eta') is a unary morphism f: x \to x' in \mathcal{M} that commutes with the multiplication and the unit. Then there is a category \mathsf{Mon}(\mathcal{M}) of monoids and monoid homomorphisms in \mathcal{M}. For example, a monoid in the multicategory of vector spaces over a field k and multilinear maps is an (associative, unital) k-algebra. A monoid in the multicategory of sets and multivariable functions is a just monoid in the standard sense.
Now, the interesting observation is that the concept of monoid is intrinsic to that of a multicategory, but in the unbiased sense of monoid:
Proof. First, notice that the terminal multicategory 1 has a single object, call it *, and has, for every arity n \geq 0, a single n-ary multimorphism, say *_n: (*, \dots, *) \to *. Composition and identities are uniquely determined.
A multifunctor F: 1 \to \mathcal{M} then consists of an object x \coloneqq F(*) in \mathcal{M} and, for every arity n \geq 0, an n-ary multimorphism \mu_n\coloneqq F(*_n): (x, \dots, x) \to x in \mathcal{M}. We have \mu_1 = 1_x since the multifunctor preserves identities, and we also have \mu_k \circ (\mu_{n_1}, \dots, \mu_{n_k}) = \mu_n \qquad\text{where}\qquad n = n_1 + \cdots + n_k since the multifunctor preserves composition. We can take this to be a definition of an unbiased monoid in the multicategory \mathcal{M}. Moreover, a natural transformation \alpha: F \Rightarrow F': 1 \to \mathcal{M} is a unary morphism f \coloneqq \alpha_*: x \to x in \mathcal{M} such that for every arity n, the square
commutes. This is a homomorphism between unbiased monoids in \mathcal{M}.
An unbiased monoid clearly gives a biased one by setting \mu \coloneqq \mu_2 and \eta \coloneqq \mu_0, whereas as a biased monoid gives an unbiased one by, for each arity n, taking \mu_n to be any composite of \mu’s and \eta’s with arity n, which can be shown to be well-defined using associativity and unitality. (That’s a baby version of a coherence theorem!) The correspondence between biased and unbiased monoids is bijective and extends to an isomorphism of categories that identifies biased and unbiased monoid homomorphisms.
So multicategories already “know” about monoids in that their generalized elements (of shape 1) are monoids! By contrast, the (1-shaped) generalized elements of a set or a category are merely elements or objects.
In category theory, monoids are most commonly internalized in a monoidal category: the ur-example of the “microcosm principle” that an algebraic structure can be interpreted inside a categorified version of itself. In our view, it is multicategories that are the most natural structure in which to internalize monoids, for several reasons. Multicategories are more general than monoidal categories; only the representable multicategories are equivalent to monoidal categories (Hermida 2000). Yet, despite being more general, multicategories are also more elementary than (weak) monoidal categories, requiring no natural isomorphisms for associativity and unitality, let alone coherence axioms going along with them.
2 2-Multicategories and pseudofunctors
This perspective on monoids immediately suggests a strategy for defining pseudomonoids and, in particular, monoidal categories: if unbiased monoids are multifunctors out of the terminal multicategory, then unbiased pseudomonoids should be pseudofunctors out of the terminal 2-multicategory. In this section, we introduce the required two-dimensional notions.
A 2-multicategory is easy to define: just as a 2-category is a category enriched in \mathbf{Cat}, a 2-multicategory is a multicategory enriched3 in \mathbf{Cat}. So a 2-multicategory \mathcal{M} has multihom-categories \mathcal{M}(x_1, \dots, x_n; y) for each list of objects x_1, \dots, x_n and y in \mathcal{M}, and the composition operations in Equation 1 are now functors rather than set maps. The prime example of a 2-multicategory is the 2-multicategory \mathcal{Cat} of categories, functors of several variables, and natural transformations.4
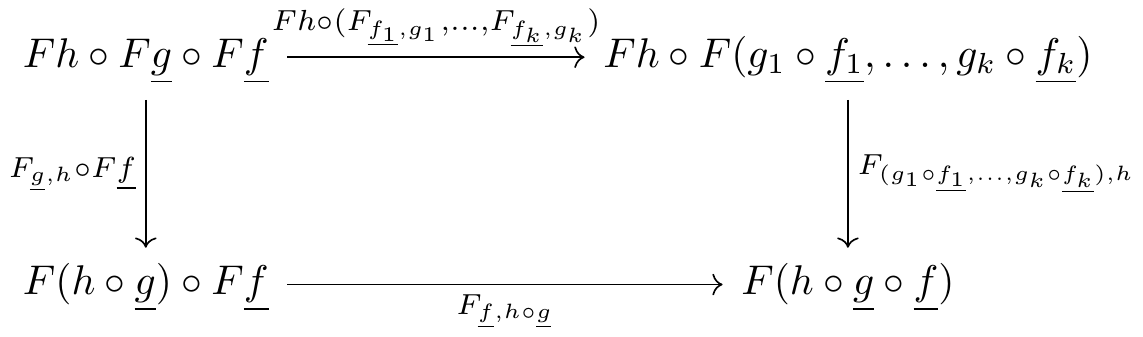
Defining a pseudofunctor between 2-multicategories takes more work, but there are no surprises. Hörmann has defined pseudofunctors between 2-multicategories with composition of multimorphisms in the “Markl-style” (g \circ_i f) (Hörmann 2018, sec. 1). Since I prefer the “May-style” composition (g \circ (f_1, \dots, f_n)) and I do not have a reference for pseudofunctors in this style, I give the definition in full.
While the coherence conditions for a lax or pseudo multifunctor are somewhat cumbersome to record, they are perfectly straightforward conceptually. At least in an intuitive sense, they are mechanically generated from the associativity and unitality axioms of a multicategory.
3 Pseudomonoids in 2-multicategories
We can now succinctly state the central definition of this post.
Here 1 denotes the terminal 2-multicategory, which is just the terminal multicategory from before regarded as a locally discrete 2-multicategory. This definition is reminiscent of the fact that a monad in a bicategory \mathbf{B} is equivalent to a lax functor 1 \to \mathbf{B}, where 1 is the terminal 2-category, although bicategories and lax functors are defined in a biased style.
As an important special case, a lax monoidal category is a lax monoid in the 2-multicategory \mathcal{Cat} and an unbiased monoidal category is a pseudomonoid in \mathcal{Cat}. So a lax monoidal category is a category \mathsf{C} equipped with functors \otimes_n: \mathsf{C}^n \to \mathsf{C}, \qquad n \geq 0, whose action on objects x_1, \dots, x_n \in \mathsf{C} might be denoted \bigotimes_{i=1}^n x_i and action on morphisms f_1: x_1 \to y_1, \dots, f_n: x_n \to y_n in \mathsf{C} denoted \bigotimes_{i=1}^n f_i: \bigotimes_{i=1}^n x_i \to \bigotimes_{i=1}^n y_i. There are also natural transformations \bigotimes_{i=1}^k \bigotimes_{j=1}^{n_i} x_{i,j} \to \bigotimes_{i=1,j=1}^{k,n_i} x_{i,j} \qquad\text{and}\qquad x \to \bigotimes_{i=1}^1 x satisfying coherence axioms for associativity and unitality. We won’t spell these out since they are immediately seen to agree with definitions already in the literature:
It is worth comparing this derivation with other ways of generating the concept of a monoidal category or its abstraction as a pseudomonoid. The best known of these is the 2-monad on the 2-category \mathbf{Cat} whose pseudo-algebras are unbiased monoidal categories. But not only do you need to know about 2-monads and their pseudo-algebras, you also need to know how to make the free strict monoidal category on a category. So, while this approach is more general, it takes quite a bit of machinery to get off the ground. The approach via 2-multicategories taken here is far more direct.
4 Commutative monoids in symmetric multicategories
As most monoidal categories encountered in practice are symmetric, we would be remiss not to explain how pseudomonoids in 2-multicategories extend to symmetric pseudomonoids in symmetric 2-multicategories. Although this might seem like a small addition, it takes about as much work to extend to symmetric pseudomonoids as to define non-symmetric pseudomonoids in the first place. So we will present the symmetric aspects in some detail. The impatient reader can skip ahead to the final section for a general discussion.
Let’s start with the one-dimensional story: commutative monoids in symmetric multicategories.
Recall that a symmetric multicategory is a multicategory with an action of the permutation groupoid on its multihom-sets. Somewhat more precisely, a symmetric multicategory is a multicategory \mathcal{M} together with operations \mathcal{M}(x_{\sigma(1)}, \dots, x_{\sigma(n)}; y) \xrightarrow{\sigma^*} \mathcal{M}(x_1, \dots, x_n; y), \qquad x_1, \dots, x_n, y \in \mathcal{M}, \tag{2} indexed by permutations \sigma: [n] \to [n] for each arity n \geq 0, which are functorial with respect to composition of permutations and compatible with composition of multimorphisms.5 A symmetric (multi)functor between symmetric multicategories \mathcal{M} and \mathcal{N} is a multifunctor F: \mathcal{M} \to \mathcal{N} whose mappings between multihom-sets are equivariant under the permutation actions, so that the square
commutes for all objects x_1,\dots,x_n,y \in \mathcal{M} and permutations \sigma: [n] \to [n]. Symmetric multicategories, symmetric multifunctors, and natural transformations form a 2-category \mathbf{sMlt}.
A (biased) commutative monoid in a symmetric multicategory \mathcal{M} is a monoid (x, \mu, \eta) in the multicategory \mathcal{M} such that \sigma^*(\mu) = \mu, where \sigma: [2] \to [2] is the swap. Commutative monoids span a full subcategory \mathsf{cMon}(\mathcal{M}) of the category of monoids in \mathcal{M}. The characterization of monoids in a multicategory extends to:
Proof. A symmetric multifunctor F: 1 \to \mathcal{M} is an unbiased monoid in \mathcal{M}, having carrier x \coloneqq F(*) and multiplications \mu_n \coloneqq F(*_n): (x,\dots,x) \to x, with the property that \sigma^*(\mu_n) = \mu_n for all permutations \sigma: [n] \to [n]. We might call this an unbiased commutative monoid in \mathcal{M}. Under the correspondence between biased and unbiased monoids in \mathcal{M}, commutative biased monoids correspond with commutative unbiased monoids. (This restricted correspondence is again a small coherence theorem! It uses the standard but not entirely trivial fact that an arbitrary permutation can decomposed into composites and sums of identities and swaps \sigma: [2] \to [2].)
So we can say that the generalized elements of symmetric multicategories are commutative monoids.
5 Symmetric 2-multicategories and symmetric pseudofunctors
Returning to the two-dimensional story, a symmetric 2-multicategory is a symmetric multicategory enriched in \mathbf{Cat}, so that the permutation actions in Equation 2 are now functors between multihom-categories. The prime example is again the symmetric 2-multicategory of categories, multivariable functors, and natural transformations. It is a symmetric 2-multicategory under the action of a permutation \sigma: [n] \to [n] on a functor F: \mathsf{C}_{\sigma(1)} \times \cdots \times \mathsf{C}_{\sigma(n)} \to \mathsf{D} given pointwise by \sigma^*(F)(x_1, \dots, x_n) \coloneqq F(x_{\sigma(1)}, \dots, x_{\sigma(n)}) and on a natural transformation \alpha: F \Rightarrow G between such functors given componentwise by \sigma^*(\alpha)_{x_1, \dots, x_1} \coloneqq \alpha_{x_{\sigma(1)}, \dots, x_{\sigma(n)}} for objects x_1 \in \mathsf{C}_1, \dots, x_n \in \mathsf{C}_n.
We now define a symmetric pseudofunctor between symmetric 2-multicategories. The coherence axioms look complicated, but again they are mechanically generated from the axioms of a symmetric multicategory (Shulman 2016, Definition 2.6.4). The permutation actions in a symmetric multicategory satisfy four equations—two expressing the functorality of the action and two expresssing its compatibility with multimorphism composition—and these give rise to the four coherence equations of a symmetric pseudofunctor.
6 Symmetric pseudomonoids in symmetric 2-multicategories
We can finally state the central definition in the symmetric case:
In particular, a symmetric lax monoidal category is a symmetric lax monoid in the symmetric 2-multicategory \mathcal{Cat} and an unbiased symmetric monoidal category is a symmetric pseudomonoid in \mathcal{Cat}. So an unbiased SMC is a unbiased monoidal category (\mathsf{C},\otimes) that is equipped with, for each permutation \sigma: [n] \to [n], a natural isomorphism B^\sigma: \sigma^* \otimes_n \Rightarrow\otimes_n: \mathsf{C}^n \to \mathsf{C} having components of form B^{\sigma}_{x_1,\dots,x_n}: \bigotimes_{i=1}^n x_{\sigma(i)} \to \bigotimes_{i=1}^n x_i, \qquad x_1, \dots, x_n \in \mathsf{C}.
These natural isomorphisms satisfy four coherence equations. For example, the functorality axiom says that
for any composable permutations [n] \xrightarrow{\sigma} [n] \xrightarrow{\tau} [n], and also that B^{1_{[n]}} = 1_{\otimes_n}. The other two coherence equations are more verbose but can be unpacked similarly.
I don’t know of a definition of an unbiased SMC in the literature that is directly comparable with this one. Brandenburg (2016) has defined a closely related notion of unbiased SMC but where the products are indexed by arbitrary finite sets, rather than just those of form [n] \coloneqq \{1,\dots,n\}. The axioms appear to be essentially the same.
7 Discussion
In summary, we’ve seen that generalized elements of multicategories are monoids and generalized elements of symmetric multicategories are commutative monoids, making (symmetric) multicategories into the natural structure for interpreting (commutative) monoids. We then categorified this situation to see that unbiased monoidal categories are “pseudo-elements” of 2-multicategories and unbiased SMCs are “pseudo-elements” of symmetric 2-multicategories. We thus recover definitions of unbiased (symmetric) monoidal categories by a conceptual route.
These are, however, only the objects of 2-categories. If unbiased monoidal categories are pseudofunctors into the 2-multicategory of categories, then we expect unbiased strong monoidal functors to be pseudonatural transformations between the pseudofunctors and unbiased monoidal transformations to be modifications between those. Checking that we obtain the 2-category of unbiased monoidal categories is a task for the future.7
It should not be lost amidst the technicalities that unbiased monoidal categories naturally capture the everyday meaning of mathematical symbols in a way that biased monoidal categories do not. When we write the expression X \times Y \times Z, we mean to have a ternary product, not an arbitrary choice of the bracketed binary products (X \times Y) \times Z or X \times (Y \times Z). Of course, as believing category theorists, we know that these objects are canonically isomorphic and so any one of them should be just as good as the others. But while this is true abstractly, it does not diminish the feeling that the elements of ternary set products should be triples (x,y,z) rather than the nested pairs ((x,y),z) or (x,(y,z)). That is exactly what unbiased monoidal products give us. The expression X \times Y \times Z can be interpreted as a conveniently chosen ternary product and, more generally, the expression X \otimes Y \otimes Z as shorthand for a ternary monoidal product \otimes_3(X,Y,Z). In informal mathematics such details are usually glossed over, but in software implementation you are forced to make specific choices of products, so you might as well make good choices. That inevitably leads to the unbiased perspective.
References
Footnotes
The slipperiness of the concept of monoidal category is borne out by its history, which starts with Bénabou giving a subtly but meaningfully wrong definition. For a brief account of this history, see John Baez’s recent expository paper about Hoàng Xuân Sính’s thesis on 2-groups (Baez 2023).↩︎
It might seem more in the spirit of multicategories to have a “natural multitransformation” \alpha: (F_1,\dots,F_n) \Rightarrow G between multifunctors \mathcal{M} \to \mathcal{N}, with a component \alpha_x: (F_1(x), \dots, F_n(x)) \to G(x) in \mathcal{N} for each x \in \mathcal{M}, but for bare multicategories, there is no such thing! In the case of symmetric multicategories, the internal hom associated with the Boardman-Vogt tensor product does yield a notion of multitransformation.↩︎
Historically speaking, enriched multicategories were the first kind to be studied. Specifically, symmetric multicategories enriched in topological spaces or simplicial sets were defined by J. Peter May and called operads (May 1972).↩︎
The 2-multicategory of multivariable functors is rarely explicitly mentioned in the literature, but it is implicitly the object of study of a fair amount of work, such as Kelly’s early papers on “many-variable functorial calculus” (Kelly 1972). More recently, 2-multicategories, double multicategories, and 2-polycategories have been used by Cheng, Gurski, and Riehl and by Shulman in the study of multivariable adjunctions.↩︎
For a complete definition of a symmetric multicategory, see (Leinster 2004, Definition 2.2.21) or (Shulman 2016, Definition 2.6.4). We follow the variance convention of the latter, which has the advantage of also working for cartesian multicategories.↩︎
By the functorality axiom, the symmetry comparisons of a symmetric lax multifunctor are always invertible. Also, a symmetric strict multifunctor usually does not have identity symmetry comparisons, just as a strict SMC (more accurately called a “symmetric strict monoidal category”) usually does not have identity braidings.↩︎
The basic ingredients should already be available in the literature: Leinster gives explicit definitions of unbiased monoidal categories, monoidal functors, and monoidal transformations (Leinster 2004, sec. 3.1) and Hörmann has precise definitions of 2-multicategories, pseudofunctors, pseudonatural transformations, and modifications (Hörmann 2018, sec. 1).↩︎