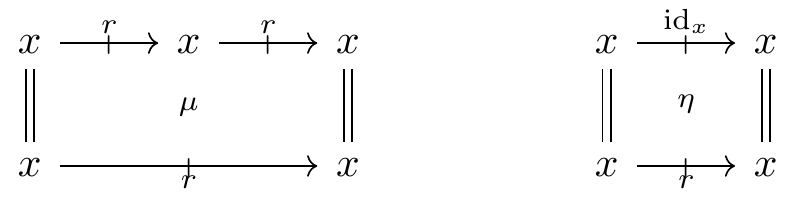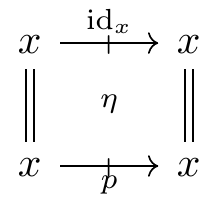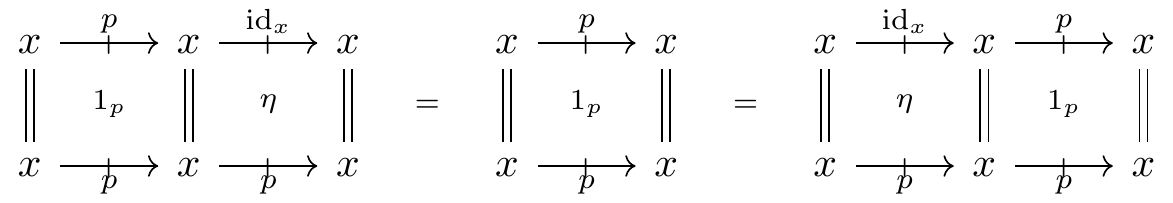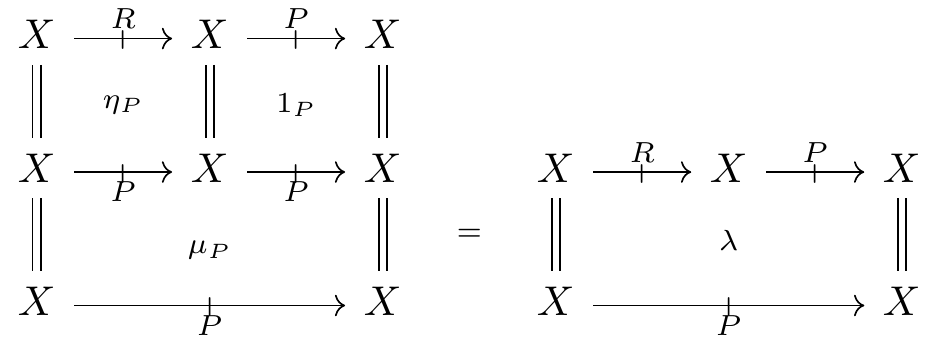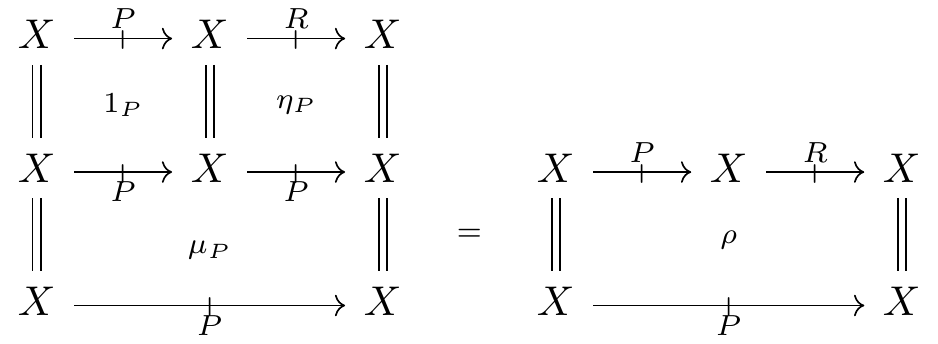Algebras are promonads

Abstract

An interesting analogy between algebras over a ring and promonads on a category is formalized using the apparatus of double theories.

You’ve probably heard the slogan that “a monad is a monoid in a category of endofunctors.” By analogy, a promonad is a monoid in a category of endoprofunctors. Or, if you prefer, a promonad is a monad in the bicategory of profunctors.¹ I found myself thinking about promonads recently, for reasons that I will reveal in the fullness of time.

On Math.SE, Bertalan Pecsi (“Berci”) made the interesting remark that a promonad on a category is analogous to an algebra over a ring. That struck me as implicitly a strong endorsement of promonads since algebras over a ring are a big deal in mathematics! The aim of this post is to formalize the analogy by showing that a suitably abstracted notion of promonad includes both promonads on categories and algebras over rings as special cases.

To accomplish this, we will exercise the machinery of double theories that Michael Lambert and I recently introduced (Lambert and Patterson 2023), building on work by Paré (2011) and others. So this post can also be read as a brisk introduction to double theories centered around a particular example. The technical level will be higher than in my ongoing series on “why double categories?” in that I will assume you’ve encountered, or are at least willing to look up, the main concepts of double category theory.

1 The module construction

Double theories are motivated by, among other things, the module construction. This construction takes a double category \mathbb{D} and produces another double category \mathbb{M}\mathsf{od}(\mathbb{D}), which is only virtual unless \mathbb{D} has certain colimits. We review the module construction here, but in a rather sketchy way since the details can be found in Leinster’s text (Leinster 2004, sec. 5.3).

Given a double category \mathbb{D}, there is a virtual double category \mathbb{M}\mathsf{od}(\mathbb{D}) whose objects, arrows, proarrows, and multicells are categories, functors, profunctors/bimodules, and multimaps of profunctors/bimodules, respectively, all internal to \mathbb{D}. But what are those? First of all, a category in \mathbb{D} consists of

• an object x in \mathbb{D}, the object carrier;
• a proarrow r: x \mathrel{\mkern 3mu\vcenter{\hbox{$\shortmid$}}\mkern-10mu{\to}}x in \mathbb{D}, the morphism carrier;
• composition and unit cells

satisfying laws of associativity and unitality. A profunctor or bimodule between categories (x,r,\mu,\eta) and (y,s,\nu,\theta) in \mathbb{D} consists of

• a proarrow m: x \mathrel{\mkern 3mu\vcenter{\hbox{$\shortmid$}}\mkern-10mu{\to}}y, and
• left and right action cells

satisfying associativity, unitality, and compatibility laws. Functors and transformations internal to \mathbb{D} are defined in a similar spirit.²

Two examples are most relevant to us, and also demonstrate the versatility of the construction. The ur-example is that, applied to the double category of spans, the module construction gives the virtual double category

\mathbb{M}\mathsf{od}(\mathbb{S}\mathsf{pan}) \simeq \mathbb{P}\mathsf{rof}

of categories, functors, profunctors, and multimaps of profunctors, which is representable as a double category via the coend formula for composing profunctors. This justifies the terminology introduced above.

For the second example, recall that a monoidal category \mathsf{M} can be regarded as a double category \mathbb{B}(\mathsf{M}) with one object and one arrow. The objects and morphisms of \mathsf{M} become the proarrows and cells of \mathbb{B}(\mathsf{M}), respectively, and the composition and monoidal product in \mathsf{M} become the internal and external composition in \mathbb{B}(\mathsf{M}). Then a category in the double category \mathbb{B}(\mathsf{M}), as defined above, is exactly a monoid in the monoidal category \mathsf{M}. Similarly, a bimodule internal to the double category \mathbb{B}(\mathsf{M}), as defined above, is a bimodule internal to the monoidal category \mathsf{M}.

Taking \mathsf{M} = (\mathsf{Ab},\otimes) to be the category of abelian groups equipped with its tensor product, the module construction on \mathbb{B}(\mathsf{M}) is the virtual double category

\mathbb{M}\mathsf{od}(\mathbb{B}(\mathsf{Ab},\otimes)) \simeq \mathbb{R}\mathsf{ing}

of rings, ring homomorphisms, bimodules over rings, and multilinear maps, which is representable as double category via the tensor product of bimodules. So we are building on the familiar fact that a ring³ is the same thing as a monoid in abelian groups. The double category of rings is an interesting one and has been studied in some detail by Paré (2021).

2 Simple double theories

You might have heard that a lax double functor \mathbb{1} \to \mathbb{S}\mathsf{pan}, where \mathbb{1} is the terminal double category, is precisely a category. More generally, for any double category \mathbb{D}, a lax functor \mathbb{1} \to \mathbb{D} is a category in \mathbb{D}, as defined above. This is a good thing to pause and think about if you haven’t seen it before, as it is a key source of intuition about lax functors. The relevant definitions and lemmas can be found in (Lambert and Patterson 2023, sec. 2).

In fact, for any pair of double categories \mathbb{D} and \mathbb{E}, there is a virtual double category \mathbb{L}\mathsf{ax}(\mathbb{D},\mathbb{E}) whose objects are lax double functors \mathbb{D} \to \mathbb{E}, and this construction generalizes the module construction in that there is an isomorphism of virtual double categories

\mathbb{M}\mathsf{od}(\mathbb{D}) \cong \mathbb{L}\mathsf{ax}(\mathbb{1}, \mathbb{D}).

The arrows in \mathbb{L}\mathsf{ax}(\mathbb{D}, \mathbb{E}) are natural transformations between lax double functors, whereas the proarrows and multicells are less familiar things called “modules” (again) and “multimodulations.” I won’t say what they are, but from the displayed isomorphism one can form the intuition that modules between lax functors are a “multi-object” generalization of profunctors between categories. For the details, see (Paré 2011) or (Lambert and Patterson 2023).

The isomorphism above suggests a generalization of the module construction. We take a small, strict double category \mathbb{T}, regarded as a kind of theory, and a (typically large) double category \mathbb{S}, by default \mathbb{S}\mathsf{pan}, regarded as the semantics. We then obtain a virtual double category \mathbb{L}\mathsf{ax}(\mathbb{T},\mathbb{S}) of models of \mathbb{T} in \mathbb{S}. Such a model, a lax functor \mathbb{T} \to \mathbb{S}, should be thought of as a family, parameterized by \mathbb{T}, of categories, functors, profunctors/bimodules, and maps thereof internal to \mathbb{S}. In this context, the double category \mathbb{T} is called a “double theory,” specifically a simple double theory to emphasize that it does not involve any extra structure on double categories, like products (Lambert and Patterson 2023, sec. 3). The terminal double category \mathbb{1} is the trivial double theory since it parameterizes a single category.

3 The theory of promonads

With that background, we return to the original idea of the post. The theory of promonads is the double category \mathbb{T}_{\mathsf{Promnd}} generated by

• an object x
• an endoproarrow p: x \mathrel{\mkern 3mu\vcenter{\hbox{$\shortmid$}}\mkern-10mu{\to}}x
• a unit cell

subject to the relations p \odot p = p and

As a consequence of the relations, the double category \mathbb{T} is not only finitely presented, but actually finite: it has exactly one object, x; one arrow, 1_x, two proarrows, \operatorname{id}_x and p; and three cells, 1_{\operatorname{id}_x} = \operatorname{id}_{1_x}, 1_p, and \eta. This is a rather special situation. Double theories are usually finitely presented but rarely finite.

4 Promonads

4.1 Promonads in a double category

Naturally, we will define a promonad to be a model of the double theory of promonads. Such models can be characterized in two useful ways.

For any double category \mathbb{S}, the following are equivalent:

1. a model in \mathbb{S} of the theory of promonads, namely a lax functor \mathbb{T}_{\mathsf{Promnd}}\to \mathbb{S};
2. a pair of categories (X,R) and (X,P) in \mathbb{S} having the same object carrier, together with a functor (1_X, H): (X,R) \to (X,P) between them that is the identity on the object carrier;
3. a category (X,R) in \mathbb{S} together with a profunctor (P,\lambda,\rho): (X,R) \mathrel{\mkern 3mu\vcenter{\hbox{$\shortmid$}}\mkern-10mu{\to}}(X,R) and multimaps of profunctors \mu_P: (P,P) \Rightarrow P and \eta_P: R \Rightarrow P such that the multiplication \mu_P is associative and the following two compatibility conditions are satisfied.

Proof

Proof (Sketch). The equivalence between (1) and (3) follows by unpacking the content of a lax double functor \mathbb{T}_{\mathsf{Promnd}}\to \mathbb{S}. To simplify the reasoning, use the lemmas in (Lambert and Patterson 2023, sec. 2). We will sketch the equivalence between descriptions (2) and (3).

Given a functor (1_X, H): (X,R) \to (X,P) in \mathbb{S} as in (2), we immediately have the multiplication \mu_P \coloneqq \mu_{(X,P)} in (3) from the composition in the category (X,P), whereas the unit \eta_P \coloneqq H: R \Rightarrow P in (3) is given by the morphism component of the functor (1_X, H). The actions \lambda and \rho are then determined by the equations above. The profunctor laws follow from the functorality of (1_X,H).

Conversely, given the data in (3), a category with object and morphism carriers X and P is defined by taking the composition \mu_{(X,P)} \coloneqq \mu_P and the unit \eta_{(X,P)} \coloneqq \eta_P \circ \eta_{(X,R)}, where \eta_{(X,R)}: \operatorname{id}_X \Rightarrow R is the unit of the given category (X,R). Associativity is immediate, and unitality follows from the compatibility equations on \lambda and \rho. We then have a functor (1,\eta_P): (X,R) \to (X,P) in \mathbb{S}, and this construction is inverse to the one above.

A promonad in a double category \mathbb{S} is defined to be any one of the above equivalent objects. In fact, promonads in \mathbb{S} are the objects of a virtual double category

\mathbb{P}\mathsf{romnd}(\mathbb{S}) \coloneqq \mathbb{L}\mathsf{ax}(\mathbb{T}_{\mathsf{Promnd}}, \mathbb{S}).

We should characterize the arrows, proarrows, and multicells of \mathbb{P}\mathsf{romnd} in a similar style, but that’s too much work for a blog post. Instead, let’s return to earth and instantiate this definition in the double categories we considered earlier, starting with the monoidal category of abelian groups.

4.2 Algebras over rings

We define the virtual double category of algebras to be

\mathbb{A}\mathsf{lg}\coloneqq \mathbb{P}\mathsf{romnd}(\mathbb{B}(\mathsf{Ab}, \otimes)).

By the proposition above, the objects of \mathbb{A}\mathsf{lg} are equivalently

• a pair of rings R and A together with a ring homomorphism f: R \to A, or
• a ring R and an R-bimodule A, along with an associative, R-bilinear multiplication \odot: A \times A \to A and an R-linear map f: R \to A such that r \cdot a = f(r) \odot a \qquad\text{and}\qquad a \cdot r = a \odot f(r), \qquad \forall r \in A,\ a \in A.

How does this definition compare with the usual one? Actually, the definition of a (noncommutative) algebra over a (noncommutative) ring is not completely standardized. It is fun to ask what it should be. The second characterization above agrees with the definition proposed by Martin Brandenburg on Math.SE. Mac Lane and Birkhoff similarly characterize algebras over a field in their textbook Algebra (Mac Lane and Birkhoff 1999, Theorem IX.23).

When both the ring and the algebra are commutative, our definition agrees with the standard one. Indeed, textbooks on commutative algebra, including those by Atiyah-MacDonald and Eisenbud, commonly define a commutative algebra to be a ring homomorphism f: R \to A between commutative rings. The halfway case of a (noncommutative) algebra A over a commutative ring R presents a subtlety. In this case, one might expect the left and right actions of R to agree, so that we have the “commutativity” equation r \cdot a = a \cdot r. This is equivalent to the ring homomorphism f: R \to A being central, meaning that the image of R lies in the center of A. That does not follow from the axioms given here.

4.3 Promonads on categories

The virtual double category of promonads without further qualification is

\mathbb{P}\mathsf{romnd}\coloneqq \mathbb{P}\mathsf{romnd}(\mathbb{S}\mathsf{pan}) = \mathbb{L}\mathsf{ax}(\mathbb{T}_{\mathsf{Promnd}}, \mathbb{S}\mathsf{pan}).

A promonad is equivalently a

• a pair of categories \mathsf{C} and \mathsf{P} with the same objects, together with an identity-on-objects functor F: \mathsf{C} \to \mathsf{P}, or
• a category \mathsf{C} and a profunctor P: \mathsf{C} \mathrel{\mkern 3mu\vcenter{\hbox{$\shortmid$}}\mkern-10mu{\to}}\mathsf{C}, along with an associative family \odot_{x,y,z}: P(x,y) \times P(y,z) \to P(x,z), \qquad x,y,z \in \mathsf{C}, of composition operations, satisfying the equations (f \cdot m) \odot n = f \cdot (m \odot n), \qquad (m \cdot g) \odot n = m \odot (g \cdot n), \qquad m \odot (n \cdot h) = (m \odot n) \cdot h, whenever they make sense for morphisms f,g,h and heteromorphisms m,n, and finally a natural transformation \eta: \operatorname{Hom}_{\mathsf{C}} \Rightarrow P satisfying the equations \eta(f) \odot m = f \cdot m \qquad\text{and}\qquad m \odot \eta(g) = m \cdot g, whenever they make sense for morphisms f,g and a heteromorphism m.

The first characterization as an identity-on-objects functor⁴ is far more succinct, but I find the second more evocative of the intuitve idea of an algebra. One might even say that a promonad on a category is an “algebra over a category.” In a future post, I will explain how this perspective can be put to good use.

5 Epilogue: change of semantics

We’ve seen that promonads on categories and algebras over rings are both instances of a single concept—more precisely, they are models of the same double theory in different semantics—but we can, if we wish, go further and place them into the same mathematical universe. While not essential to the main thread of the post, this epilogue illustrates an important feature of double theories: the ease of changing of semantics. In general, flexibility in the choice of semantics is one of the big advantages of functorial semantics. In case of the double-functorial semantics, it generalizes change of base for enriched categories.

For any distributive monoidal category \mathcal{V}, there is a double category {\mathcal{V}}\text{-}\mathbb{M}\mathsf{at} of sets, functions, \mathcal{V}-valued matrices, and transformations of \mathcal{V}-matrices. Taking \mathcal{V}= (\mathsf{Set},\times), the double category of set-valued matrices is equivalent to the double category of spans of sets, \mathbb{M}\mathsf{at}\simeq \mathbb{S}\mathsf{pan}. Thus, a promonad over a category can equally be viewed as a model of \mathbb{T}_{\mathsf{Promnd}} in \mathbb{M}\mathsf{at}, and if anything that is more faithful to the description given previously. The other case of interest, the monoidal category \mathcal{V}= (\mathsf{Ab},\otimes) of abelian groups with its tensor product, leads to the virtual double category

\mathbb{M}\mathsf{od}({\mathsf{Ab}}\text{-}\mathbb{M}\mathsf{at}) \simeq \mathsf{Ab}\text{-}\mathbb{P}\mathsf{rof}= \mathbb{R}\mathsf{ingoid}

whose objects are either categories enriched over abelian groups or ringoids, depending on whether you prefer to emphasize their “category-like” or “ring-like” aspect.

Any lax monoidal functor F: \mathcal{V}\to \mathcal{W} between distributive monoidal categories \mathcal{V} and \mathcal{W} induces a lax double functor

F_*: {\mathcal{V}}\text{-}\mathbb{M}\mathsf{at} \to {\mathcal{W}}\text{-}\mathbb{M}\mathsf{at}

that is the identity on objects and arrows and acts on \mathcal{V}-matrices and their transformations entrywise by F. In particular, the free abelian group functor F: \mathsf{Set}\to \mathsf{Ab} extends to a lax monoidal functor F: (\mathsf{Set},\times) \to (\mathsf{Ab},\otimes) and, in turn, to a lax double functor F_*: \mathbb{M}\mathsf{at}\to {\mathsf{Ab}}\text{-}\mathbb{M}\mathsf{at}. Our first change of semantics sends a promonad on a category, or lax functor M: \mathbb{T}_{\mathsf{Promnd}}\to \mathbb{M}\mathsf{at}, to the composite

\mathbb{T}_{\mathsf{Promnd}}\xrightarrow{M} \mathbb{M}\mathsf{at}\xrightarrow{F_*} {\mathsf{Ab}}\text{-}\mathbb{M}\mathsf{at},

which is a promonad in the double category of abelian group-valued matrices.

There is also, for any distributive monoidal category \mathcal{V}, a (pseudo) double functor G: \mathbb{B}(\mathcal{V}) \to {\mathcal{V}}\text{-}\mathbb{M}\mathsf{at} that sends the unique object of \mathbb{B}(\mathcal{V}) to the singleton set and each object x of \mathcal{V} to the one-by-one \mathcal{V}-matrix with entry x. Taking \mathcal{V}= (\mathsf{Ab},\otimes), another change of semantics sends an algebra over a ring, or lax functor M': \mathbb{T}_{\mathsf{Promnd}}\to \mathbb{B}(\mathsf{Ab}), to the composite

\mathbb{T}_{\mathsf{Promnd}}\xrightarrow{M'} \mathbb{B}(\mathsf{Ab}) \xrightarrow{G} {\mathsf{Ab}}\text{-}\mathbb{M}\mathsf{at}.

So, promonads over categories and algebras over rings can both be seen as “algebroids over ringoids,” in the first case by freely adding formal sums and in the second by viewing algebras over rings as algebroids over ringoids, both with one object. While neither identification is very surprising at this point, double-functorial semantics makes achieving them as simple as post-composition.

References

Lambert, Michael, and Evan Patterson. 2023. “Cartesian Double Theories: A Double-Categorical Framework for Categorical Doctrines.” https://arxiv.org/abs/2310.05384.

Leinster, Tom. 2004. Higher Operads, Higher Categories. Cambridge University Press. https://doi.org/10.1017/CBO9780511525896.

Mac Lane, Saunders, and Garrett Birkhoff. 1999. Algebra. 3rd ed. American Mathematical Society.

Paré, Robert. 2011. “Yoneda Theory for Double Categories.” Theory and Applications of Categories 25 (17): 436–89. http://www.tac.mta.ca/tac/volumes/25/17/25-17abs.html.

———. 2021. “Morphisms of Rings.” Joachim Lambek: The Interplay of Mathematics, Logic, and Linguistics, 271–98. https://doi.org/10.1007/978-3-030-66545-6_8.

Street, Ross, and Elango Panchadcharam. 2007. “Mackey Functors on Compact Closed Categories.” Journal of Homotopy and Related Structures 2 (2): 261–93. https://arxiv.org/abs/0706.2922.

Footnotes

1. While hardly a famous concept, promonads on enriched categories have occasionally been invoked by Street and collaborators, for example in (Street and Panchadcharam 2007, sec. 12). The related idea of an “arrow” has been studied independently by programming language theorists.

2. It is worth noting, though, that these last two definitions, unlike the first two, involve nonidentity arrows in the double category \mathbb{D}, hence cannot be fully realized in a bicategory.

3. In this post, all rings have units and ring homomorphisms preserve units.

4. One might also worry that an identity-on-objects functor refers to categories that “have the same objects” and so violates the principle of equivalence. But whether that is so depends on one’s perspective. To avoid this problem, the nLab suggests that an identity-on-objects functor be defined as a category enriched in the arrow category of \mathsf{Set}. Alternatively, our second characterization also respects the principle of equivalence. Notice that the latter formulations, via enriched categories and double theories, both treat identity-on-object functors as objects, whereas naively such functors are morphisms between categories. The distinction is meaningful: given a pair of categories, it violates the principle of equivalence to ask whether they have same objects, but given a set of objects, it is perfectly acceptable to put two different category structures on it.