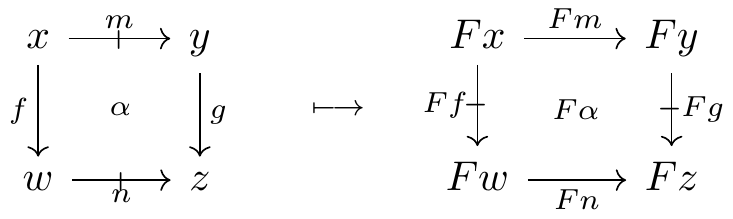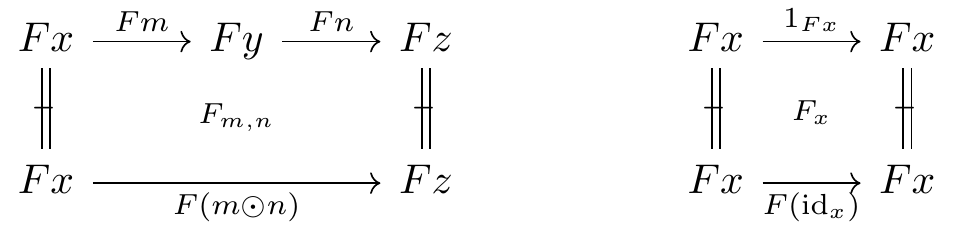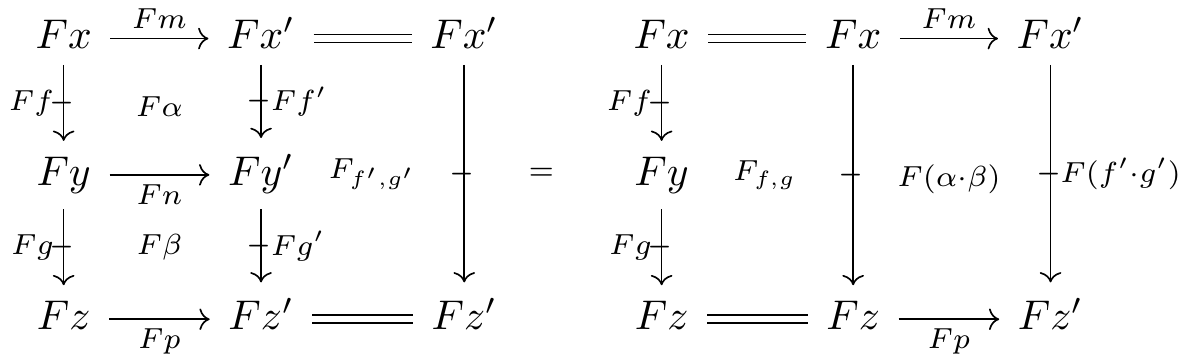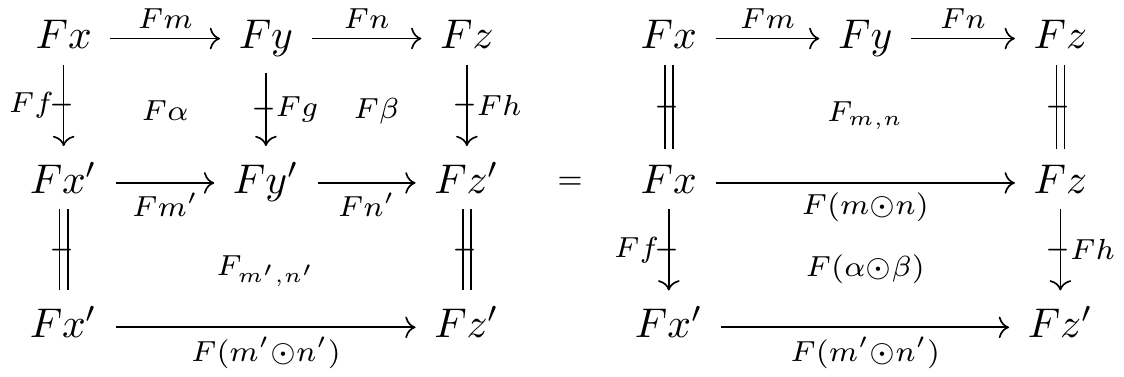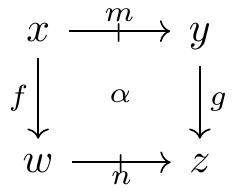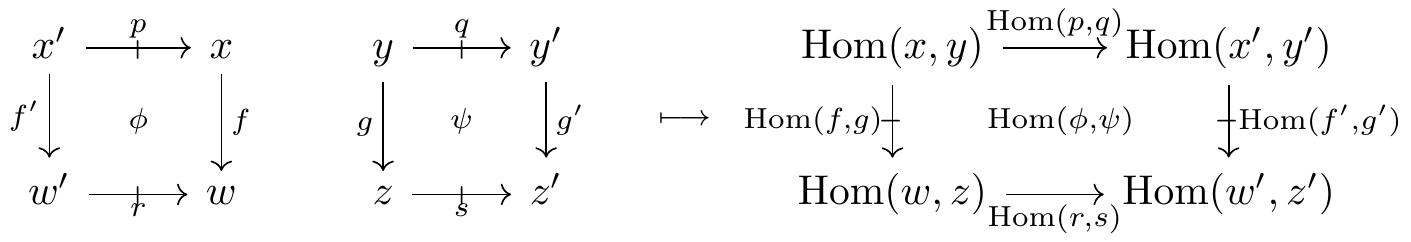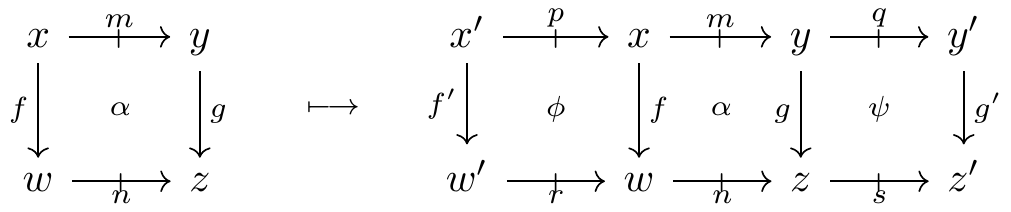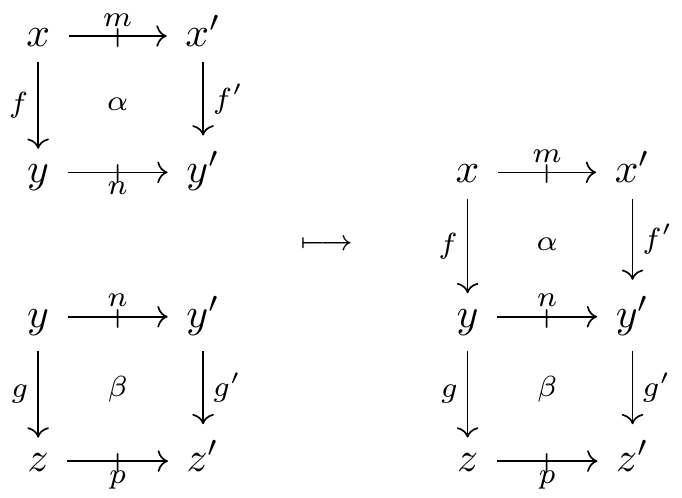Toward compact double categories: Part 1
The twisted Hom double functor
Lately I’ve been pursuing formal category theory using double categories. A first step in this program is to abstract from categories to category objects in a double category; for instance, internal categories are category objects in a double category of spans and enriched categories are category objects in a double category of matrices. The next step is to take structures defined on categories and generalize them to category objects in a double category. By the microcosm principle, that is possible when the double category possesses a categorified version of the very structure in question. The concepts from double category theory that I’ve used so far, like products and coproducts, indeed categorify familiar concepts from category theory. While there are interesting twists along the way,1 the one-dimensional story gives strong hints about how to generalize to double categories.
An operation on categories that has no direct analogue for sets is taking the opposite category. Though trivial to compute—simply turn the arrows around—the existence of a nontrivial symmetry on categories has the powerful consequence that every definition or result in the language of category theory has a dual. Ideas in category theory come at a two-for-the-price-of-one bargain. Opposites also occur constantly in everyday use of category theory, such as when taking a contravariant functor to be a (covariant) functor out of an opposite category.
An abstract account of categorical duality is thus essential for formal category theory: what structure must a double category possess for its category objects to admit a duality? Unfortunately, for all its apparent simplicity, categorical duality has resisted a satisfactory axiomatization. Ideally, we would find universal properties that determine the opposite category uniquely, at least up to equivalence. Let’s begin by seeing how a purely bicategorical approach founders.
1 The compact bicategory of profunctors
A basic property of the opposite category is that for any categories \mathsf{X}, \mathsf{Y}, and \mathsf{Z}, profunctors \mathsf{X} \times \mathsf{Y} \mathrel{\mkern 3mu\vcenter{\hbox{$\shortmid$}}\mkern-10mu{\to}}\mathsf{Z} naturally correspond with profunctors \mathsf{X} \mathrel{\mkern 3mu\vcenter{\hbox{$\shortmid$}}\mkern-10mu{\to}}\mathsf{Y}^\mathrm{op}\times \mathsf{Z}. This property should remind you of how, for any finite-dimensional vector spaces U, V, and W, linear maps U \otimes V \to W naturally correspond with linear maps U \to V^* \otimes W, where V^* is the dual vector space of V. In the case of profunctors, the correspondence is captured by a compact closed bicategory (Carmody 1995; Stay 2016), or compact bicategory for short,2 the bicategorical analogue of a compact category. Specifically, under the set-theoretic cartesian product, categories, profunctors, and natural transformations form a symmetric monoidal bicategory (\mathbf{Prof}, \otimes). It becomes a compact bicategory when the dual of a category is taken to be its opposite, as observed by Day and Street (1997).
Yet compact bicategories fall short of axiomatizing categorical duality via universal properties, in two ways.
First, a symmetric monoidal product is a structure on, not a universal property of, a bicategory. A purely bicategorical fix would be to use cartesian bicategories instead of monoidal bicategories, but as I have argued on this blog and in print (Patterson 2024), cartesian or finite-product double categories are more elegant solutions, being defined by simpler universal properties. So double categories already neatly solve this problem.
Second—and this is the problem that will occupy us—even once the symmetric monoidal structure on the bicategory is fixed, duals are defined by a bicategorical universal property, which is too loose in key examples. In the case of profunctors, the universal property gives equivalences of hom-categories
\mathbf{Prof}(\mathsf{X} \otimes \mathsf{Y}, \mathsf{Z}) \simeq \mathbf{Prof}(\mathsf{X}, \mathsf{Y}^* \otimes \mathsf{Z}).
In particular, taking both \mathsf{X} and \mathsf{Z} to be \mathsf{1}, we have that the categories of presheaves on \mathsf{Y} and of copresheaves on \mathsf{Y}^* are equivalent. The general case gives no further information. Thus, the dual category \mathsf{Y}^* is determined by the universal property up to Morita equivalence, under which two categories are considered to be the same if any of the following equivalent conditions hold:
- the categories have equivalent categories of presheaves
- the categories are equivalent in the bicategory \mathbf{Prof}
- the Cauchy completions of the categories are equivalent (in \mathbf{Cat}).
So, if I asked you for the dual of a category, you would be allowed to take its opposite and then also take its Cauchy completion. But wait, that’s not what I asked for! To make this more vivid, the nLab notes that the Cauchy completion of the category of open subsets of Euclidean spaces and smooth maps is the category of smooth manifolds. If those two categories were the same, differential geometry wouldn’t be a subject!
The second problem cannot be solved in the same way as the first. In the first case, the trouble is that the bicategory \mathbf{Prof} cannot detect the familiar universal property of products, since it holds with respect to tight morphisms in the double category \mathbb{P}\mathsf{rof}. But categorical duality really is a universal property with respect to loose morphisms in \mathbb{P}\mathsf{rof}. So one has to wonder whether double categories can help here at all. In this series of posts I will point out that, perhaps surprisingly, double categories do help in key examples, even if the general story remains mysterious to me.
2 Outline
With that preamble, our aim is to propose a definition of a compact double category.3 The definition will involve an adjunction in the loose direction of the double category, generalizing an adjunction in a bicategory. As far as I know, this notion of double adjunction has not yet been defined; the elegant theory of double adjunctions created by Grandis and Paré (1999) refers to the tight direction. To define such adjunctions, I will employ a version of the Hom double functor, but again, the Hom double functor from the Yoneda theory for double categories (Paré 2011) refers to the tight direction. Continuing to work backwards, to cook up this “twisted” Hom functor, which sends arrows to proarrows and vice versa, I will need similarly “twisted” notion of double functor.
So that’s where we will begin in the next section: defining a twisted lax functor between double categories. We then construct our motivating example, the twisted Hom functor on a double category. Only in the next post will get back to our original objective.
The upfront cost in machinery is admittedly high, but I find these ancillary ideas interesting in their own right and I believe they will find other uses. Still, everything explored here should be considered provisional.
3 Twisted double functors
The transpose of a strict double category \mathbb{D} is a new double category \mathbb{D}^\top that exchanges the categories of horizontal and vertical morphisms, thus transposing the cells. That this is possible is a special situation. In general, a double category4 cannot be transposed due to the fundamental asymmetry of being strict in one direction and weak in the other. Nevertheless, it can be interesting to consider “double functors” \mathbb{D} \to \mathbb{E}^\top that behave like double functors from \mathbb{D} into the transpose of \mathbb{E}, even when the transpose makes no formal sense. I call these “twisted double functors.”
Definition 1 A twisted lax double functor F: \mathbb{D} \to \mathbb{E}^\top between double categories \mathbb{D} and \mathbb{E} consists of an assignment sending
- each object x of \mathbb{D} to an object Fx of \mathbb{E},
- each arrow f: x \to y of \mathbb{D} to a proarrow Ff: Fx \mathrel{\mkern 3mu\vcenter{\hbox{$\shortmid$}}\mkern-10mu{\to}}Fy of \mathbb{E},
- each proarrow m: x \mathrel{\mkern 3mu\vcenter{\hbox{$\shortmid$}}\mkern-10mu{\to}}y of \mathbb{D} to an arrow Fm: Fx \to Fy of \mathbb{E}, and
- each cell of \mathbb{D} to a cell of \mathbb{E}, as follows:
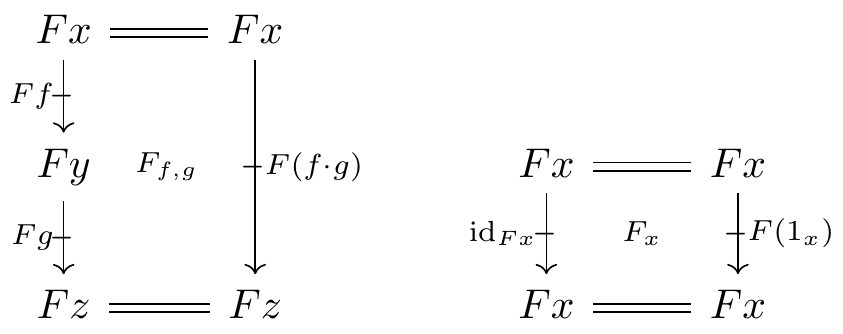
In addition, for composable arrows x \xrightarrow{f} y \xrightarrow{g} z and for objects x in \mathbb{D}, there are composition and identity comparison cells in \mathbb{E}:
Similarly, for composable proarrows x \ \overset{m}{\mathrel{\mkern 3mu\vcenter{\hbox{$\shortmid$}}\mkern-10mu{\to}}}\ y \ \overset{n}{\mathrel{\mkern 3mu\vcenter{\hbox{$\shortmid$}}\mkern-10mu{\to}}}\ z and for objects x in \mathbb{D}, there are comparison cells in \mathbb{E}:
This data must satisfy the following axioms.
Naturality of composition comparisons, in both directions: for internally composable cells \alpha and \beta in \mathbb{D},
and for externally composable cells \alpha and \beta in \mathbb{D},
Naturality of unitality comparisons, in both directions: analogous.
Associativity and unitality of composition and identity comparisons, in both directions: two instances of the usual associativity and unitality axioms for a lax functor; cf. (Grandis 2019, Definition 3.5.1).
Notice that, when the domain \mathbb{D} is strict, a twisted lax functor \mathbb{D} \to \mathbb{E}^\top is more general than an ordinary lax functor \mathbb{D}^\top \to \mathbb{E}, and when the codomain \mathbb{E} is strict, it is more general than an ordinary lax functor \mathbb{D} \to \mathbb{E}^\top, because a twisted lax functor is lax in both directions. For our purposes, laxness with respect to arrows, captured by the comparisons F_{f,g}, is the more essential feature, but in our main example we must at least allow a twisted functor to be pseudo with respect to proarrows, so that the comparisons F_{m,n} are non-identity cells invertible with respect to external composition in \mathbb{E}.
The rules for composing ordinary and twisted lax functors deserve more attention than I’ve given them. For now, I’ll just say that twisted lax functors can be precomposed with ordinary ones. Specifically, given a lax functor H: \mathbb{C} \to \mathbb{D} and a twisted lax functor F: \mathbb{D} \to \mathbb{E}^\top, there is another twisted lax functor F \circ H: \mathbb{C} \to \mathbb{E}^\top.
4 The twisted Hom functor
In his “Yoneda theory for double categories,” Paré (2011) introduces the Hom double functor
\operatorname{Hom}: \mathbb{D}^\mathrm{op}\times \mathbb{D} \to \mathbb{S}\mathsf{pan},
in which \mathbb{D}^\mathrm{op} is the tight dual of \mathbb{D}, reversing its arrows and cells. The Hom functor is a lax double functor that sends a pair of objects x and y in \mathbb{D} to the hom-set \operatorname{Hom}(x,y) := \mathbb{D}_0(x,y) consisting of arrows x \to y, as usual, and sends a pair of proarrows m: x \mathrel{\mkern 3mu\vcenter{\hbox{$\shortmid$}}\mkern-10mu{\to}}y and n: w \mathrel{\mkern 3mu\vcenter{\hbox{$\shortmid$}}\mkern-10mu{\to}}z in \mathbb{D} to the span
\operatorname{Hom}(m,n) := \big( \mathbb{D}_0(x,w) \xleftarrow{s} \mathbb{D}_1(m,n) \xrightarrow{t} \mathbb{D}_0(y,z) \big)
whose apex is the set of cells m \Rightarrow n. The action on arrows and cells is given by composition in \mathbb{D}_0 and \mathbb{D}_1, respectively, and the comparison cells are given by external composition and identities in \mathbb{D}. In this way, the Hom double functor faithfully encodes all the operations of a double category.
Most parallel and economical would be to define a “twisted Hom functor” of the form
\operatorname{Hom}: \mathbb{D}^\mathrm{co}\times \mathbb{D} \xrightarrow{?} \mathbb{S}\mathsf{pan}^\top,
in which \mathbb{D}^\mathrm{co} is the loose dual of \mathbb{D}, reversing its proarrows and cells. However, \mathbb{S}\mathsf{pan} is too strict to make this definition: composition of proarrows in a double category \mathbb{D} obeys the category laws only up to natural isomorphism, whereas the only cells in \mathbb{S}\mathsf{pan} that could furnish these composition comparisons are identities!5 The twisted Hom functor must be valued in \mathbb{P}\mathsf{rof} instead. That is arguably preferable anyway since, following the philosophy of pseudo double categories, proarrows are first and foremost the objects of a category and thus it would violate the principle of equivalence to not at least retain their globular isomorphisms.
Definition 2 The twisted Hom double functor on a double category \mathbb{D} is the twisted lax functor
\operatorname{Hom}: \mathbb{D}^\mathrm{co}\times \mathbb{D} \to \mathbb{P}\mathsf{rof}^\top
that maps
each pair of objects x and y in \mathbb{D} to the hom-category \mathbb{D}(x,y) comprising the proarrows x \mathrel{\mkern 3mu\vcenter{\hbox{$\shortmid$}}\mkern-10mu{\to}}y and globular cells between them;
each pair of arrows f: x \to w and g: y \to z in \mathbb{D} to the profunctor between hom-categories
\operatorname{Hom}(f,g): \operatorname{Hom}(x,y) \mathrel{\mkern 3mu\vcenter{\hbox{$\shortmid$}}\mkern-10mu{\to}}\operatorname{Hom}(w,z)
in which the heteromorphisms from a proarrow m: x \mathrel{\mkern 3mu\vcenter{\hbox{$\shortmid$}}\mkern-10mu{\to}}y to another w \mathrel{\mkern 3mu\vcenter{\hbox{$\shortmid$}}\mkern-10mu{\to}}z are just the cells in \mathbb{D} of form
on which globular cells act by pre- and post-composition;
each pair of proarrows p: x' \mathrel{\mkern 3mu\vcenter{\hbox{$\shortmid$}}\mkern-10mu{\to}}x and q: y \mathrel{\mkern 3mu\vcenter{\hbox{$\shortmid$}}\mkern-10mu{\to}}y' in \mathbb{D} to the functor between hom-categories
\operatorname{Hom}(p,q): \operatorname{Hom}(x,y) \to \operatorname{Hom}(x',y')
that sends a proarrow m: x \mathrel{\mkern 3mu\vcenter{\hbox{$\shortmid$}}\mkern-10mu{\to}}y to the composite proarrow p \odot m \odot q: x' \mathrel{\mkern 3mu\vcenter{\hbox{$\shortmid$}}\mkern-10mu{\to}}y' and a globular cell \alpha: m \Rightarrow n to the composite cell 1_p \odot \alpha \odot 1_q;
each pair of cells in \mathbb{D} as on the left
to the natural transformation on the right whose component \operatorname{Hom}(\phi,\psi)_{m,n} at a pair of proarrows m: x \mathrel{\mkern 3mu\vcenter{\hbox{$\shortmid$}}\mkern-10mu{\to}}y and n: w \mathrel{\mkern 3mu\vcenter{\hbox{$\shortmid$}}\mkern-10mu{\to}}z in \mathbb{D} is given by external composition:
The comparison cells of the twisted Hom functor are defined as follows. At pairs of composable arrows x \xrightarrow{f} y \xrightarrow{g} z and x' \xrightarrow{f'} y' \xrightarrow{g'} z' in \mathbb{D}, the composition comparison \operatorname{Hom}_{(f,f'),(g,g')} is the natural transformation whose components act by composition in \mathbb{D}_1:
The identity comparison \operatorname{Hom}_{(x,x')} at a pair of objects x and x' in \mathbb{D} is just the identity on the hom-category \mathbb{D}(x,x').
Finally, at pairs of composable proarrows x'' \ \overset{p'}{\mathrel{\mkern 3mu\vcenter{\hbox{$\shortmid$}}\mkern-10mu{\to}}}\ x' \ \overset{p}{\mathrel{\mkern 3mu\vcenter{\hbox{$\shortmid$}}\mkern-10mu{\to}}}\ x \qquad\text{and}\qquad y \ \overset{q}{\mathrel{\mkern 3mu\vcenter{\hbox{$\shortmid$}}\mkern-10mu{\to}}}\ y' \ \overset{q'}{\mathrel{\mkern 3mu\vcenter{\hbox{$\shortmid$}}\mkern-10mu{\to}}}\ y'' in \mathbb{D}, the composition comparison \operatorname{Hom}_{(p,q),(p',q')} is the natural isomorphism whose component at m: x \mathrel{\mkern 3mu\vcenter{\hbox{$\shortmid$}}\mkern-10mu{\to}}y is the globular isomorphism
p' \odot (p \odot m \odot q) \odot q \cong (p' \odot p) \odot m \odot (q \odot q')
given by the associators of \mathbb{D}. Similarly, the identity comparison \operatorname{Hom}_{(x,y)} at a pair of objects x and y in \mathbb{D} is the natural isomorphism whose component at m: x \mathrel{\mkern 3mu\vcenter{\hbox{$\shortmid$}}\mkern-10mu{\to}}y is the globular isomorphism
m \cong \operatorname{id}_x \odot m \odot \operatorname{id}_y
given by the unitors of \mathbb{D}.
This completes the construction of the twisted Hom functor. We crucially used that it is valued in profunctors, not spans, when defining the final comparison cells. The twisted Hom functor is, in fact, a twisted normal lax functor, meaning that the identity comparisons in both directions are isomorphisms. Like the ordinary Hom functor, the twisted Hom functor faithfully encodes all the operations of a double category, but now in a transposed fashion.
Next time, we put the twisted Hom functor to work, defining a compact double category using a twisted double adjunction.
References
Footnotes
There are at least two plausible and useful double-categorical analogues of cartesian categories: “cartesian double categories” (Aleiferi 2018) and “double categories with finite products” (Patterson 2024). Furthermore, the latter tend to exhibit a laxness with no 1-categorical counterpart.↩︎
A “compact bicategory” is sometimes taken to mean something different, namely a bicategory in which every morphism has a left and a right adjoint. In this series of posts we will only ever use “compact” to mean “compact closed.”↩︎
Compact double categories have been contemplated by various people over the years, but so far no entirely definite proposal has emerged. On the nLab, Shulman has sketched an interesting unbiased approach to compact double categories and compact virtual double categories. Further afield, Niefield (2024) studies cartesian closed double categories, which are closed in the tight direction, not the loose one.↩︎
I follow the convention that double categories and double functors are pseudo by default.↩︎
In the jargon of (Aleiferi 2018, Definition 4.3.7), the double category \mathbb{S}\mathsf{pan} is unit-pure: any cell between identity spans must itself be the external identity on a function. Thus, a twisted Hom functor valued in spans could only be defined for strict double categories. By contrast, the double category \mathbb{P}\mathsf{rof} is not unit-pure: the cells bounded by identity profunctors are arbitrary natural transformations between functors.↩︎