How to write a fantastic book in four months, Part I
In the first post of this series, we introduce the freely available online book Relational Thinking: from abstractions to applications, starting with the story of how it came into being and giving a brief overview of its contents.
This is a recent experiment at Topos and the results turned out fantastic, hence we would like to share with the entire world how to write a fantastic book in four months. Let us clarify, when we say a fantastic book, we mean an interactive book built using modern technology.
Somewhere in November 2023, Brendan and Priyaa set out on a mission to write an inclusive online book on the programming library AlgebraicJulia intended for a general STEM-oriented audience. Our motto for the book was to inspire and empower.
The end product of this mission was an online book titled “Relational Thinking: from abstractions to applications” crafted by a team of four including Paul Dancstep and Angeline Aguinaldo.
Even though this book is on category theory, we decided to use a friendlier term “Relational thinking” and made it the title of the book:
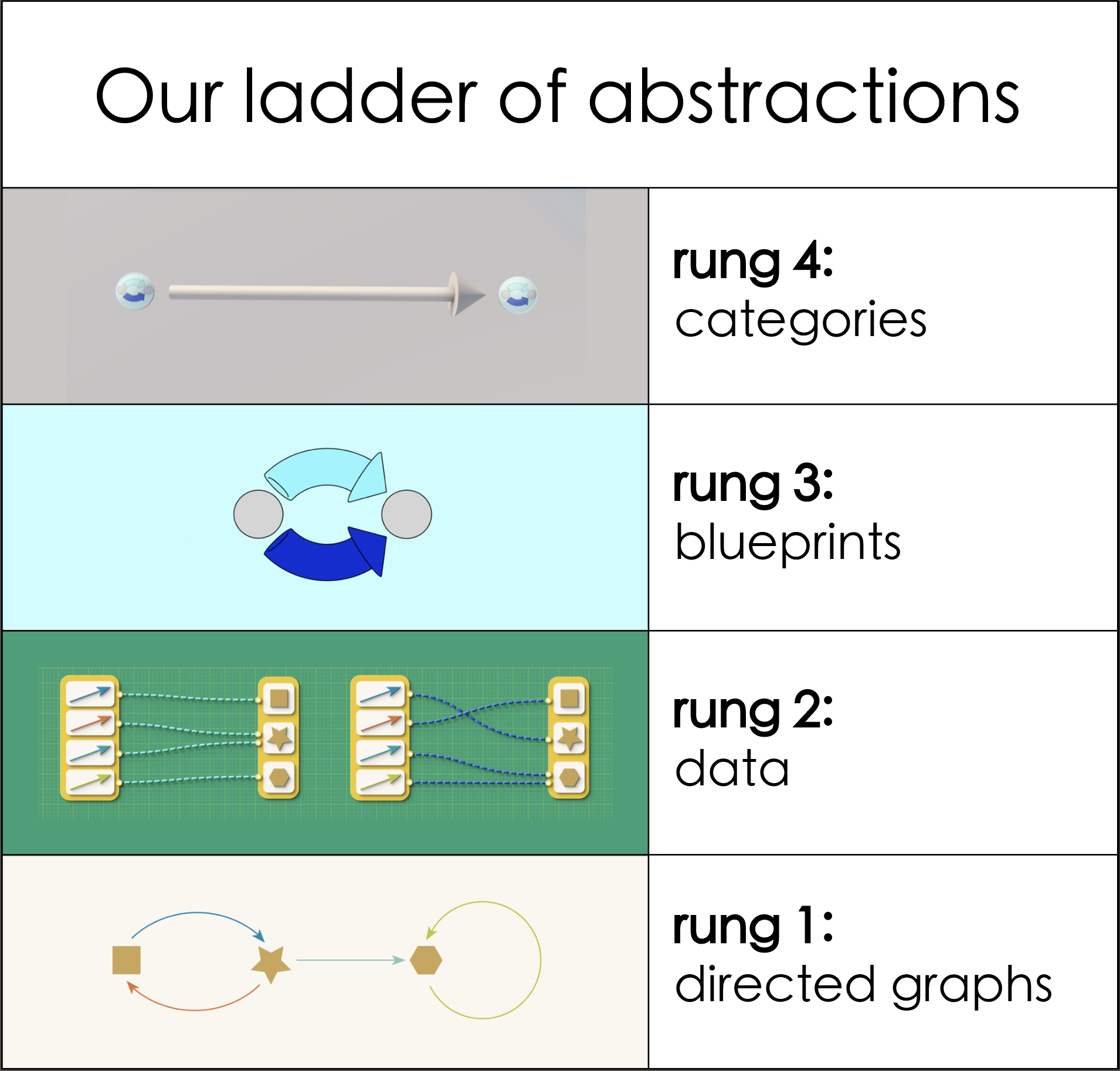
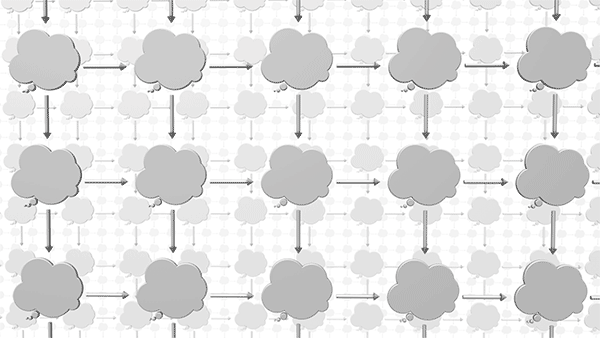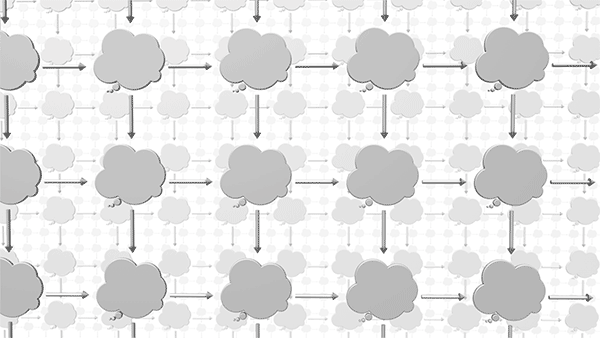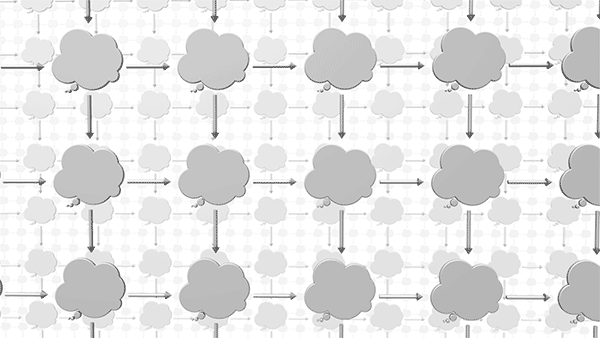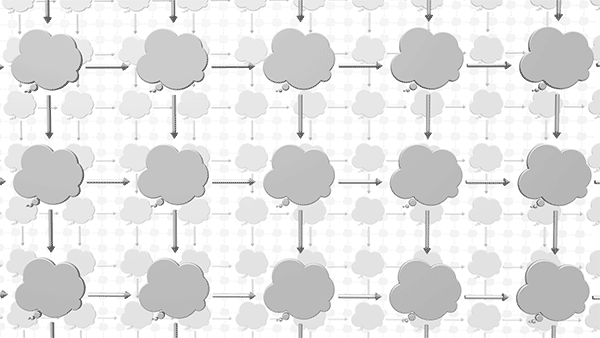
The picture below captures the crux of the book:
We chose directed graphs (shown in rung 1) as our tool to demonstrate relational thinking. The book slowly takes the reader through a ladder where at each step directed graphs are progressively abstracted from being a visual tool to a powerful computational tool. As we move up the ladder of abstraction, the focus organically shifts from graphs to relationships between graphs.
When we reach the top of the ladder in Chapter 6, we realize that we have ended up in the category of graphs and graph morphisms with a solid sense of what a category is!
In this process of climbing the ladder of abstraction, we do not spell out any formal definition of category or directed graph. Rather we rely on invoking the imagination of the reader and building instincts for these concepts based on common-sense. Little did we know that down this road, we would meet universal properties and get a completely different view of them (in Chapter 6) without requiring to meet functors and natural transformations.
Thinking deeply about categories and universal properties in this manner revealed a few cool insights as to what is being formalized by the mathematics:
“Universal property is a mathematical name for harmony of relationships.”
“Commuting diagrams are like ecosystems in balance. When multiple ecosystems are pasted together along their edges, any change in one ecosystem will create a change in the other. When the most natural information flows along the morphisms, all the ecosystems are in balance.”
We see these insights to play out well when we describe double pushout rewriting on graphs in Chapter 7. Again the focus is not on just double pushouts but a reflection on the thinking process behind the double pushouts and its application. At the end of Chapter 7, we can’t help but noticing that relational thinking is good thinking!
We conclude the chapter by observing that relational thinking shifts our vocabulary as well as eliminates the need to be clever.
Chapter 8 demonstrates some surprising and cool applications of double pushout rewriting in real-world science.
We originally intended the book to have four or five chapters. But, when we finished we realized that we have a beautiful nine chapters of a complete journey (Our chapters start from number zero).
If you are wondering, “Wait a minute, I thought this is a book on AlgebraicJulia!”, well, you see, it actually is! All the category theory concepts introduced in the book intuitively are brought to life using AlgebraicJulia.
Throughout the book, there are code snippets of AlgebraicJulia operationalizing the mathematical concepts introduced. These code snippets can be executed in the browser (no need for new installations) and are also editable.
We made a decision of wanting the readers to experience the utility of AlgebraicJulia rather than learning how to code it in it. For more ambitious readers, we have also uploaded the code in a GitHub repository: ToposInstitute/RelationalThinking-code.
We hope that this post motivates you enough to have a peek at the content as well as the cool features of the book!
Our original intention behind this post was to share about a few open-source technologies that made this book possible. But, we shall save it for the sequel!