We explore these questions in two research tracks: Accountable Sense-making and Networked Mathematics.
Accountable Sense-making
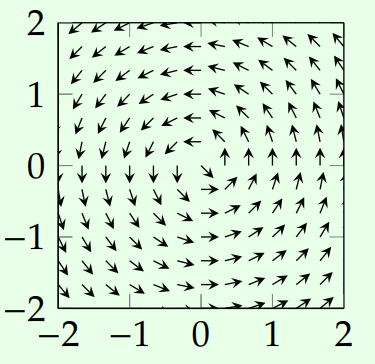
In this track, we develop precise mathematics, via polynomial functors, for understanding dynamical systems, decision processes, information pipelines and working languages. We want to find answers to the following questions.
- How do we make sense of things? Is that related to the way we sense things?
- How does communication work? What allows different entities (e.g. different database schemas) to communicate?
- What is the hierarchical nature of work, planning, prediction and learning?
- Is there a flexible and elegant language for talking about all of the above?
Networked Mathematics
In this track, we use natural language processing and formal logical inference to organize mathematical knowledge relationally and make cutting-edge research as well as standard mathematics more accessible.
A cornerstone of accessibility is search, and math is not easy to search. Indeed, a group of physicists discovered a useful identity in linear algebra but could not find previously published instances of the result despite asking experts.
On the flip side, how many useful identities are known by experts, but not accessible to physicists, engineers and others? Some are simple calculations that don’t fit in a traditional paper. Some may only be useful if the right person comes along with the right question.
We make the case for having all known mathematics available to everyone in accessible formats. This starts by having mathematical concepts and their relationships organized in useful ways.
Mathematical literature is growing quickly (3% yearly with 120,000 new papers in 2017) but our infrastructure for organizing and communicating these results has not kept up. The ramifications are significant: wasted search time, duplication of research, and missed connections between fields.
To mitigate these effects, we employ three strategies.
- Apply recent advances in natural language processing (NLP) and knowledge representation (e.g. word embeddings, transformers, generative AI) to mathematical literature.
- Improve the organization and dissemination of math with NLP-powered tools (e.g. search engines, knowledge graphs, ontologies) and good user interfaces.
- Connect the lexical semantics generated by NLP approaches with the logical semantics generated by proof assistants (e.g. Lean, Coq, Isabelle, HOL).
Highlights
Categorical systems theory
Categorical Systems Theory is an open-access book on using category theory to model complex systems, focussing on new ways of describing rich interfaces between individual people and parts. We formally define dynamical systems, systems theories, and systems doctrines.

Data sets
With collaborators at NIST, “Extracting Mathematical Concepts from Text” is a preliminary study into organizing mathematical knowledge with AI techniques, in order to make cutting-edge math research more accessible. We also release data sets for training and testing.
MathGloss
MathGloss creates a glossary and knowledge graph for undergraduate mathematics from text, automatically using modern NLP tools and resources already available on the web.
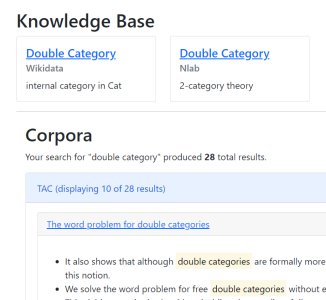
Parmesan
Traditional NLP methods perform poorly when searching for and defining mathematical concepts in context. Parmesan is a hybrid system that addresses the issues explicitly in Category Theory by concept/relation/definition extraction, and entity linking. This forms part of the larger MathFoldr project.
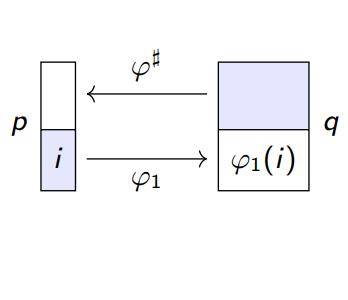
Poly at Work
We believe that Poly is a springboard for progress at the intersection of mathematics and computing. At the annual Poly at Work workshop, theoretical and applied researchers get together to solve Poly-shaped problems, and become more fluent in using Poly to articulate the things they care about.
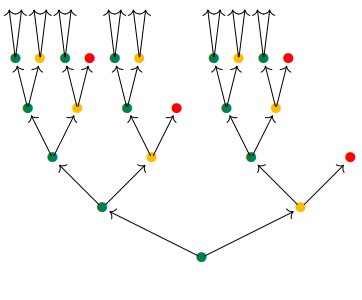
Poly book
Polynomial Functors: A General Theory of Interaction is an open-access textbook and lecture course on polynomial functors, a mathematical framework for describing interaction, dynamical systems, and decision-making. This provides the foundation for much of our work on intelligence and cooperation.
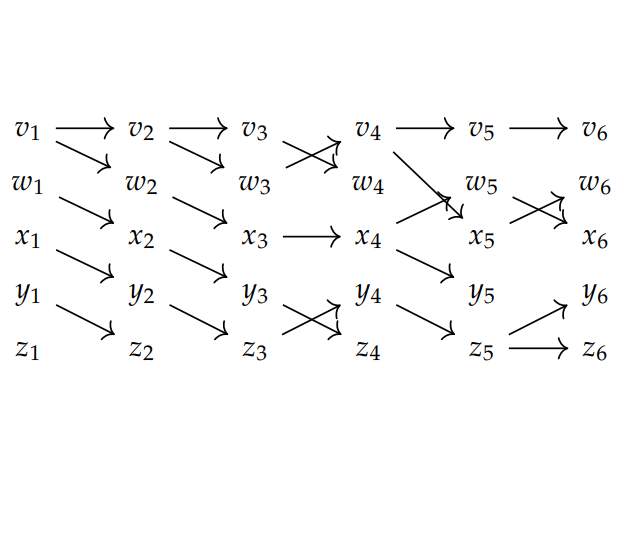
Working language
“Structure and dynamics of working language” is a new project that extends prior work on polynomial functors and dynamics to account for how language works, in the sense of basic physics: it directs energy transfer, leading to the displacement of material objects in space.
No matching items
Select publications
Collard, Jacob, Valeria de Paiva, Brendan Fong, and Eswaran Subrahmanian. 2022.
“Extracting Mathematical Concepts from Text.” In
The 8th Workshop on Noisy User-generated Text.
https://arxiv.org/abs/2208.13830.
Collard, Jacob, Valeria de Paiva, and Eswaran Subrahmanian. 2023.
“Parmesan: Mathematical Concept Extraction for Education.” https://arxiv.org/abs/2307.06699.
Horowitz, Lucy, and Valeria de Paiva. 2023.
“MathGloss: Building mathematical glossaries from text.” https://arxiv.org/abs/2311.12649.
Jaz Myers, David. 2023.
Categorical Systems Theory.
http://davidjaz.com/Papers/DynamicalBook.pdf.
Niu, Nelson, and David I. Spivak. 2021a.
“Collectives: Compositional protocols for contributions and returns.” https://arxiv.org/abs/2112.11518.
———. 2021b.
“Polynomial Functors: A General Theory of Interaction.” https://topos.institute/poly-course/.
Paiva, Valeria de, Qiyue Gao, Pavel Kovalev, and Lawrence S. Moss. 2023.
“Extracting Mathematical Concepts with Large Language Models.” https://arxiv.org/abs/2309.00642.
Shapiro, Brandon, and David I. Spivak. 2022.
“Dynamic categories, dynamic operads: From deep learning to prediction markets.” https://arxiv.org/abs/2205.03906.