Nate & Jesse’s adjoint 5-tuple
In August, Nate Soares visited the Topos Institute. We told him a little about Poly and Proly, and he told us about what he wanted from a type theory. Probably the high point in the discussion for me is when he drew the following picture of what he wanted from a type theory.
1 Introduction
In August, Nate Soares visited Topos Institute. We told him a little about \mathbf{Poly} and \mathbf{Proly} and he told us about what he’d been working on with his colleague Jesse Liptrap. Probably the high point in the discussion for me is when he drew the following picture of what they wanted from a type theory:1
The picture has several stray marks, but the idea is that there should be a pair of categories, one noted \mathbf{Ctx} and one noted \sum_{C:\mathbf{Ctx}}\mathbf{Ty}\ C, as well as an adjoint quintuple between them. Every context has an empty type, “0s”; given a context and type we can extract just the context, “fst”; every context has a terminal type, “1s”; given a context and a type we can extend the context with the type to get a new context, (unlabeled in the picture); and given a context we can weaken it and thus consider it a type in the empty context, “Wk”. These are the five adjoints. One model of this that Nate suggested is to have \mathbf{Ctx}=\mathbf{Set} and \mathbf{Ty}\ C=\mathbf{Fun}(C,\mathbf{Set}).
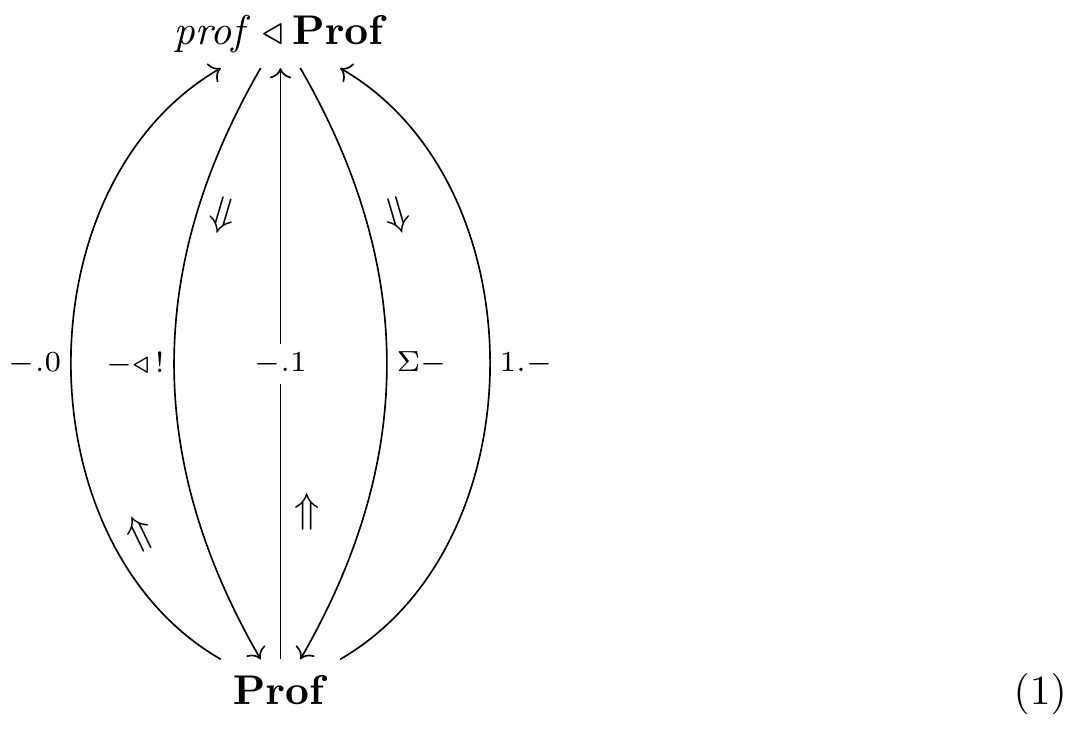
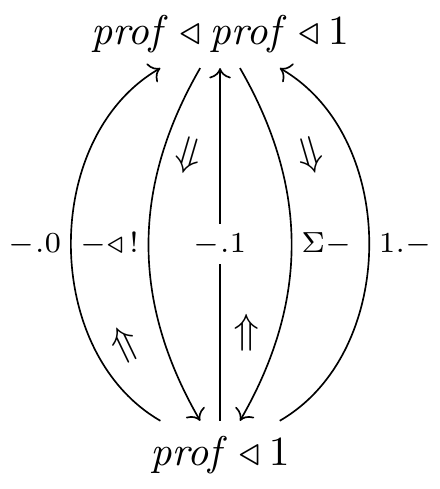
In my own search for a type theory suitable for the kind of work I want to do, I came across prolynomials, which are pairs (\mathcal{C},\mathcal{D}) where \mathcal{C} is a category and \mathcal{D}\colon\mathcal{C}\to\mathbb{P}\mathbf{rof} is a normal pseudofunctor. Letting \mathbf{Prof} be the 1-category of categories and isomorphism classes of profunctors, there is an “identity” pseudofunctor \mathbf{Prof}\to\mathbb{P}\mathbf{rof},2 and I denote the corresponding prolynomial by \mathit{prof}. Below, I’ll explain the meaning of the following adjoint 5-tuple, in which all three upward functors are fully faithful and which seems to offer a richer model of Nate’s requirements for a type theory:3
Below I’ll also give my rendition of a type theory for this adjoint 5-tuple and then explain how \Pi\colon\mathit{prof}\mathbin{\triangleleft}\mathbf{Prof}\to\mathbf{Prof} comes in.
All this is work in progress, and proofs have not been carefully written down. Thanks to Brandon Shapiro for useful conversations as always!
2 Categories indexing categories and profunctors
Let’s start from the beginning: suppose \mathcal{C} is a category. We consider \mathcal{C}-indexed families of categories and profunctors, i.e. functors \mathcal{D}\colon\mathcal{C}\to\mathbf{Prof}. To every object C or morphism c\colon C_1\to C_2 in \mathcal{C}, it assigns a category \mathcal{D}C or a profunctor \mathcal{D}c\colon\mathcal{D}C_1\nrightarrow\mathcal{D}C_2 \frac{C:\mathop{\mathrm{Ob}}\mathcal{C}}{\mathcal{D}C\colon\mathbf{Cat}} \quad \frac{C_1\xrightarrow[]{c}C_2:\mathop{\mathrm{Mor}}\mathcal{C}}{\mathcal{D}C_1\overset{\mathcal{D}c}{\nrightarrow}\mathcal{D}C_2:\text{Profunctor}} \tag{2} If you want to conceptualize the whole thing, you can “draw a picture” of it by taking the Grothendieck construction of \mathcal{D}, which I’ll denote \Sigma\mathcal{C}.\mathcal{D} \frac{\mathcal{C}:\mathbf{Cat}\quad\mathcal{D}\colon\mathcal{C}\to\mathbf{Prof}}{\Sigma\mathcal{C}.\mathcal{D}:\mathbf{Cat}} It is the category4 with objects and morphisms given as follows: \begin{aligned} \mathop{\mathrm{Ob}}(\Sigma\mathcal{C}.\mathcal{D})&\coloneqq \{(C,D)\mid C\in\mathop{\mathrm{Ob}}\mathcal{C}, D\in\mathop{\mathrm{Ob}}\mathcal{D}C\} \\ (\Sigma\mathcal{C}.\mathcal{D})\big((C_1,D_1),(C_2,D_2)\big)&\coloneqq \{(c,d)\mid c\colon \mathcal{C}(C_1, C_2), d\colon (\mathcal{D}c)(D_1,D_2)\} \end{aligned} There is a functor \sum\mathcal{C}.\mathcal{D}\to\mathcal{C} that sends (C,D)\mapsto C and (c,d)\mapsto c. This functor is called a Giraud-Conduché fibration—i.e. an exponentiable map in \mathbf{Cat}—and it generalizes both Grothendieck fibrations and Grothendieck opfibrations. Over every object C\in\mathcal{C} sits a whole category \mathcal{D}C, and over every map in \mathcal{C} sits a whole profunctor. But this last sentence is true for any functor \mathcal{X}\to\mathcal{C}, not just when \mathcal{X} is a walking object or arrow mapping into \mathcal{C}. The thing that makes an exponentiable map more well-behaved can be seen when \mathcal{X} is a path of length 2: for any composable maps C_0\xrightarrow[]{c_1}C_1\xrightarrow[]{c_2}C_2, we have \mathcal{D}(c_1\mathbin{;}c_2)\cong \mathcal{D}(c_1)\mathbin{;}\mathcal{D}(c_2).
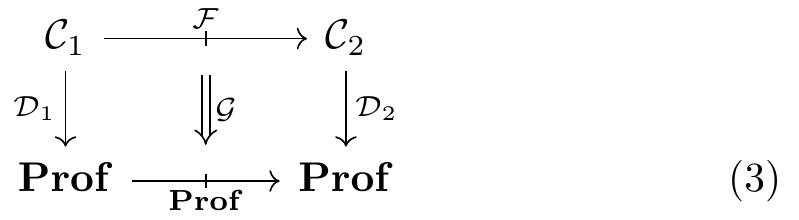
Now consider what happens if we have two such things \mathcal{D}_1\colon\mathcal{C}_1\to\mathbf{Prof} and \mathcal{D}_2\colon\mathcal{C}_2\to\mathbf{Prof} and a profunctor \mathcal{C}_1\overset{\mathcal{F}}{\nrightarrow}\mathcal{C}_2 between their indexing categories. To make \mathcal{F} coherent with \mathcal{D}_1 and \mathcal{D}_2, and hence find a good notion of morphism, one can consider diagrams—taken in a large enough double category \mathbb{P}\mathbf{rof} of categories, functors, and profunctors—that has either of the following forms
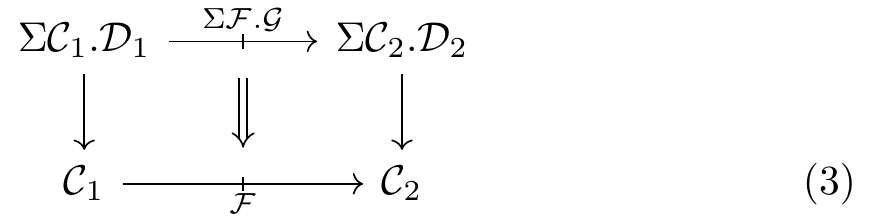
or equivalently
which are equivalent via the Grothendieck construction \Sigma. Such a morphism (\mathcal{F},\mathcal{G}) consists of a system of profunctors indexed by \mathcal{C}_1 and \mathcal{C}_2:5 \frac{C_1:\mathop{\mathrm{Ob}}\mathcal{C}_1\quad C_2:\mathop{\mathrm{Ob}}\mathcal{C}_2\quad F\colon\mathcal{F}(C_1,C_2)}{\mathcal{D}_1C_1\overset{\mathcal{G}F}{\nrightarrow}\mathcal{D}_2C_2:\text{Profunctor}} \tag{4}
Now let’s take stock of what we’ve done in this section. To each category \mathcal{C} we have given a category, namely that of functors \mathcal{C}\to\mathbb{P}\mathbf{rof}. And for each profunctor \mathcal{F}\colon\mathcal{C}_1\nrightarrow\mathcal{C}_2 we have given a profunctor between these categories, namely the one sending (\mathcal{D}_1,\mathcal{D}_2) to the set of diagrams as in (3). Our next job is to connect this situation to what’s going on in Diagram (1).
3 Explaining the adjoint 5-tuple
In (1) we see two categories, \mathbf{Prof} and \mathit{prof}\mathbin{\triangleleft}\mathbf{Prof}. Recall that \mathit{prof} is the prolynomial that sends \mathcal{X}:\mathbf{Cat} to the category whose object set is \mathop{\mathrm{Ob}}\mathit{prof}(\mathcal{X})\coloneqq\{(\mathcal{C},D)\mid\mathcal{C}:\mathbf{Cat}, D\colon\mathcal{C}\to\mathcal{X}\} A morphism (\mathcal{C}_1,D_1)\to(\mathcal{C}_2,D_2) in \mathit{prof}(\mathcal{X}) consists of a profunctor \mathcal{F}\colon\mathcal{C}_1\nrightarrow\mathcal{C}_2 and a 2-cell
By setting \mathcal{X}=1, we see that \mathit{prof}\mathbin{\triangleleft}1=\mathit{prof}(1)=\mathbf{Prof}. What is \mathit{prof}\mathbin{\triangleleft}\mathit{prof}\mathbin{\triangleleft}1=\mathit{prof}(\mathbf{Prof})? It is what we get by making \mathcal{X}=\mathbf{Prof}. An object in it is a pair (\mathcal{C},\mathcal{D}) where \mathcal{C} is a category and \mathcal{D}\colon\mathcal{C}\to\mathbf{Prof}, and a morphism is exactly what we have above in (3)! So we see that the situation described in §2 describes the category \mathit{prof}\mathbin{\triangleleft}\mathbf{Prof}.
Thus we now understand the top and bottom objects, \mathit{prof}\mathbin{\triangleleft}\mathit{prof}\mathbin{\triangleleft}1=\mathit{prof}\mathbin{\triangleleft}\mathbf{Prof} and \mathit{prof}\mathbin{\triangleleft}1=\mathbf{Prof}, in (1):
To explain the five functors, let \mathbf{0} be the empty category and let \mathbf{1} be the 1-morphism category; each is classified by a functor 1\to\mathbf{Prof}=\mathit{prof}\mathbin{\triangleleft}1, or equivalently by a prolynomial map, namely \ulcorner\mathbf{0}\urcorner,\ulcorner\mathbf{1}\urcorner\colon \mathcal{y}\to\mathit{prof}. Thus we obtain the first (leftmost) functor, which is more pedantically written \mathit{prof}\mathbin{\triangleleft}\ulcorner\mathbf{0}\urcorner\mathbin{\triangleleft}1 and the third (middle) functor \mathit{prof}\mathbin{\triangleleft}\ulcorner\mathbf{1}\urcorner\mathbin{\triangleleft}1 above. The unique functor \,!\colon\mathit{prof}\mathbin{\triangleleft}1\to 1 gives rise to the second functor. The Grothendieck construction \Sigma defines the fourth functor. And the fifth functor is given by \ulcorner\mathbf{1}\urcorner\mathbin{\triangleleft}\mathbf{Prof}.
Thus we have explained the adjoint 5-tuple that Nate recognized as important for type theory.
Note that (\mathit{prof},1,\Sigma) is a monad in \mathbb{P}\mathbf{roly}. Although it hasn’t been proven, it appears that there is a distributive law \aleph\colon\mathit{prof}\mathbin{\triangleleft}\mathit{prof}\to\mathit{prof}\mathbin{\triangleleft}\mathit{prof}. Composing with 1 and then projecting we get \mathit{prof}\mathbin{\triangleleft}\mathit{prof}\mathbin{\triangleleft}1\xrightarrow[]{\aleph\mathbin{\triangleleft}1}\mathit{prof}\mathbin{\triangleleft}\mathit{prof}\mathbin{\triangleleft}1\xrightarrow[]{\mathit{prof}\mathbin{\triangleleft}\,!}\mathit{prof}\mathbin{\triangleleft}1 This is well-named as \Pi, the dependent product, and I believe that \aleph extends the distributive law \mathit{set}^\textnormal{op}\mathbin{\triangleleft}\mathit{set}\to\mathit{set}\mathbin{\triangleleft}\mathit{set}^\textnormal{op} defining the free distributive completion 2-monad \mathbf{FreeDist}\colon\mathbf{Cat}\to\mathbf{Cat}, but I’ll leave this for another time. If you want intuition on dependent products and how they relate to distributive laws, see my blog post Jump monads: from conjugation to dependent types from last year.
4 Type theory for the adjoint 5-tuple
I’m not a type theorist, so take this with a grain of salt. But here is something like a type theory for the adjoint 5-tuple, whose upward functors are fully faithful.
The diagram (1) determines type constructors:
\frac{P:(\mathit{prof}\mathbin{\triangleleft}\mathbf{Prof})}{P\mathbin{\triangleleft}\,!:\mathbf{Prof}}
\qquad
\frac{P:(\mathit{prof}\mathbin{\triangleleft}\mathbf{Prof})}{\Sigma P:\mathbf{Prof}}
\tag{5}
\frac{A:\mathbf{Prof}}{A.0:(\mathit{prof}\mathbin{\triangleleft}\mathbf{Prof})}
\qquad
\frac{A:\mathbf{Prof}}{A.1:(\mathit{prof}\mathbin{\triangleleft}\mathbf{Prof})}
\qquad
\frac{A:\mathbf{Prof}}{1.A:(\mathit{prof}\mathbin{\triangleleft}\mathbf{Prof})}
\tag{6}
satisfies the following rules:
\frac{A:\mathbf{Prof}}{A\equiv (A.0)\mathbin{\triangleleft}\,!}
\qquad
\frac{A:\mathbf{Prof}}{(A.1)\mathbin{\triangleleft}\,!\equiv A}
\qquad
\frac{A:\mathbf{Prof}}{A\equiv\Sigma(A.1)}
\qquad
\frac{A:\mathbf{Prof}}{\Sigma(1.A)\equiv A}
\tag{7}
has the following derivations:
\frac{P:(\mathit{prof}\mathbin{\triangleleft}\mathbf{Prof})}{\mathrm{incl}: (P\mathbin{\triangleleft}\,!).0\to P}
\qquad
\frac{P:(\mathit{prof}\mathbin{\triangleleft}\mathbf{Prof})}{\mathrm{repr}\colon P\to(P\mathbin{\triangleleft}\,!).1}
\qquad
\frac{P:(\mathit{prof}\mathbin{\triangleleft}\mathbf{Prof})}{\mathrm{relx}\colon(\Sigma P).1\to P}
\tag{8}
\frac{P:(\mathit{prof}\mathbin{\triangleleft}\mathbf{Prof})}{\mathrm{lift}\colon P\to 1.\Sigma P}
\qquad
\frac{P:(\mathit{prof}\mathbin{\triangleleft}\mathbf{Prof})}{\mathrm{empt}\colon(\Sigma P).0\to P}
\qquad
\frac{P:(\mathit{prof}\mathbin{\triangleleft}\mathbf{Prof})}{\mathrm{chop}\colon P\to 1.(P\mathbin{\triangleleft}\,!)}
\tag{9}
satisfying the usual triangle identities for the adjunctions.
5 Conclusion
The category of categories and profunctors is very important in category theory. Here we’ve considered categories \mathcal{C} that index these things: for each object C:\mathcal{C} you get a category \mathcal{D}C and for each morphism c\colon C\to C' you get a profunctor \mathcal{D}(c): \mathcal{D}(C) \to \mathcal{D}(C'). between them. When you put all these together, allowing \mathcal{C} to change via profunctors, you get something that \mathbf{Proly} calls \mathit{prof}\mathbin{\triangleleft}\mathbf{Prof}. And by forgetting the \mathcal{D} stuff, you get a map \mathit{prof}\mathbin{\triangleleft}\mathbf{Prof}\to\mathbf{Prof} that has a left adjoint, a right adjoint, a right adjoint to that, and a right adjoint to that! These define some of the basic constructions that one may want in a type theory.
In a future post (or paper) we plan to write out a string diagram language that makes all of these five adjoints, plus the map \aleph that gives rise to the dependent product \Pi, quite easy to reason about. But for now, we’re simply marking this adjoint 5-tuple stepping stone we’ve found—with Nate’s guidance—that might help us think better about dynamic interacting systems in the future.
Footnotes
In the white board picture, the “0s” functor is labeled in black because, unlike the orange arrows, Nate does not consider it strictly necessary for a good type theory.↩︎
One deals with size issues in the usual way, with a hierarchy of universes that one climbs each time one needs to. Here not only is \mathbf{Prof} a 1-category \mathbf{Prof} and \mathbb{P}\mathbf{rof} a bicategory (or double category), \mathbf{Prof} is smaller than \mathbb{P}\mathbf{rof} in that it includes only the small objects.↩︎
There’s a prolynomial corresponding to the functor \mathbf{Set}\to\mathbf{Prof} that sends each set S to the corresponding discrete category. Nate’s suggestion at the top would be to replace \mathit{prof} by \mathit{set} and \mathbf{Prof} by \mathbf{Set}, giving rise to the adjoint 5-tuple on the left
commuting along the evident inclusion \mathit{set}\to\mathit{prof} of discrete categories and functors between them. I would really love to see this diagram formalized in a proof assistant.↩︎
Since the morphisms in \mathbf{Prof} are isomorphism classes of profunctors and we took \mathcal{D}\colon\mathcal{C}\to\mathbf{Prof} to land there, we technically only have defined the category \Sigma\mathcal{C}.\mathcal{D} up to an identity-on-objects isomorphism. If we demand all of the sets \mathcal{D}F(D,D') in our profunctors be equipped with a well-order, i.e. a bijection to some ordinal, then we would get an actual choice of category \Sigma\mathcal{C}.\mathcal{D} here. We implicitly assume that going forward: for each \mathcal{D}\in\mathbf{Prof} the sets \mathcal{D}(D_1,D_2) found in \mathbf{Prof} are considered to be ordinals. This is for example the approach of Kapulkin-Lumsdaine.↩︎
This system of profunctors satisfies the requirement that for any F\colon\mathcal{F}(C_1,C_2) and maps c_1\colon C_1'\to C_1 and c_2\colon C_2\to C_2' one has \mathcal{G}((\mathcal{D}_1c_1)\mathbin{;}(\mathcal{G}F)\mathbin{;}(\mathcal{D}_2c_2))=\mathcal{G}(c_1\mathbin{;}F\mathbin{;}c_2).↩︎