Categorical Statistics in Julia
This summer I created the StatisticalTheories.jl package so we can do categorical probability and synthesize probabilistic programs in the AlgebraicJulia ecosystem. Read all about it!
My project this summer was to implement the statistical theories from Evan’s thesis (Patterson 2020) and connect them to the world of probabilistic programming in the brand new AlgebraicJulia package StatisticalTheories.jl.
1 What is a statistical theory and why do we care?
The motivation here is that we are attempting to construe traditional statistical models as instances of some sort of functorial semantics, and statistical theories answer what the domain of such a functor is.
To begin with, a Markov category (Fritz 2020) is a semicartesian symmetric monoidal category equipped with a copy operation. A Statistical Theory is then a small Markov category T with a distinguished morphism p:\theta\to X which is thought of as the sampling morphism.
A Statistical Model is a functor from a statistical theory to a suitable semantics category. In our case we are looking at the Kleisli category of the Giry monad on some category of vector spaces, but the semantic category can (and usually does) have additional structure as well. Concretely, the morphisms of such a category are Markov kernels, which can be thought of as generalizations of Markov process transition matrices to an infinite state space.
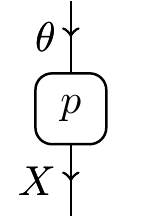
The initial statistical theory only has \theta,X, and p in it:
A model of this could refer to many things, like the outcome of a dice roll or the temperature on a given day or the number of snaggleteeth a given crocodile has, depending on what model of the theory we choose. What’s important is that statistical theories tell us about the structure of such scenarios.
But the initial theory is a little boring, what about something else?
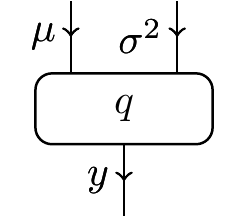
Well, we can define a linear theory which has parameters \mu and \sigma^2:
One could imagine that a model of this theory might send q to the kernel which sends (\mu,\sigma^2) to \mathcal{N}(\mu,\sigma^2). So this is cool, we’ve made something a bit more expressive than the initial theory.
But what if we want to do a regression?
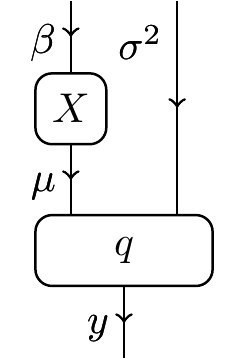
The statistical theory for a linear regression on a datum is as follows:
Now, a model of this theory will also have to specify a design morphism X, which holds the data (in this case this morphism would traditionally map $M$ for some design matrix M). As the shape of the design matrix is unspecified, this allows a lot of structural degrees of freedom in the model. This is antithetical to the purpose of functorial semantics.
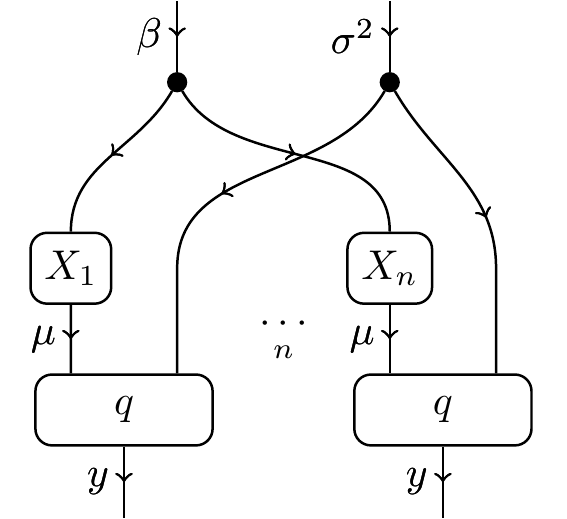
If we want to sequester more of the structure in the theory, we need something like this:
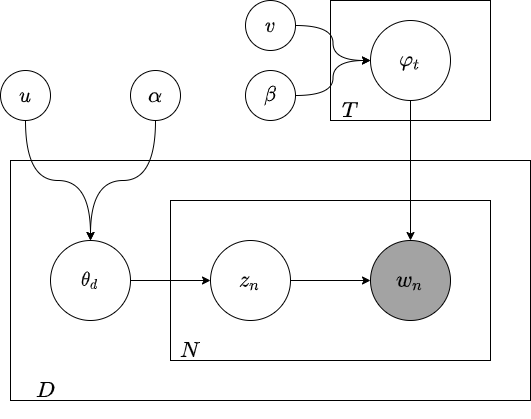
which allows us to do multivariate stuff. Intuitively, the meaning of an ellipsis in a string diagram makes sense. It means “put n of them in parallel,” right? In statistics, a string diagram with an ellipsis is illustrated using plates, and called a plate diagram:
Notably, plate diagrams can be nested hierarchically as well:
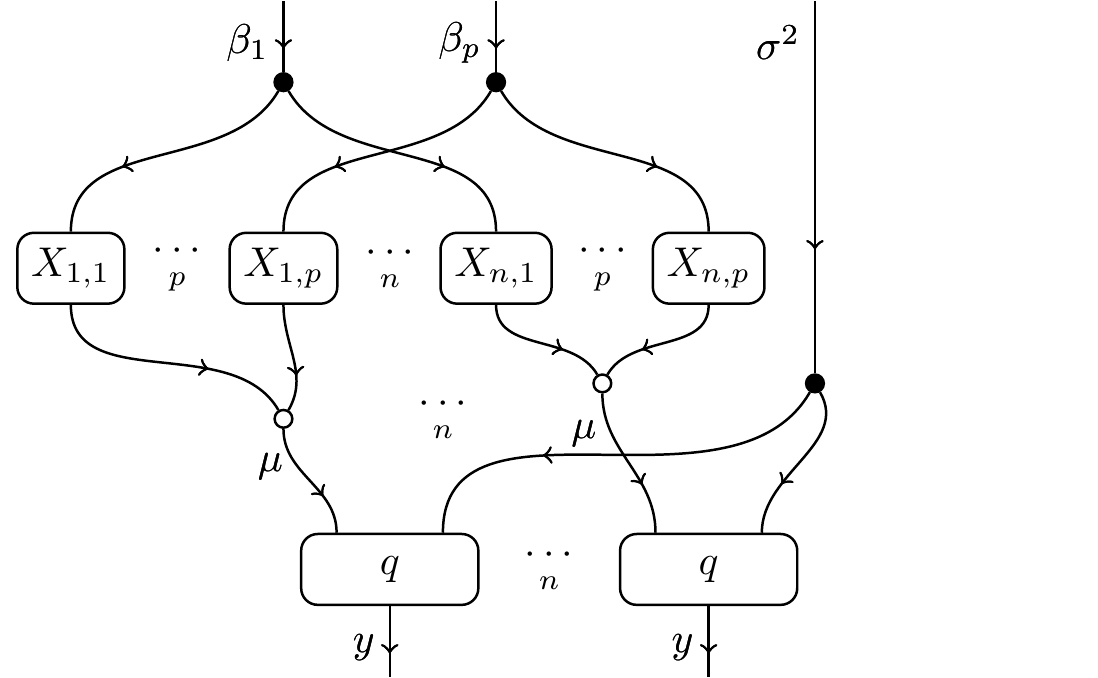
A “simple” hierarchical case is that of linear models on p predictors and n observations, where we want to do the same thing to each of the n observations, and that thing is to weight the predictors by some parameters and make a normal distribution out of them:
A more complicated example is that of a school district. Say there are a number of schools, each with a number of classrooms, each with a number of students. These numbers differ across schools and classrooms, and perhaps we also want to maintain unique parameters and/or global parameters within/across schools, classrooms, and students. This model would have several levels of hierarchy.
How would we talk about a theory for such a model categorically?
2 Plate Diagrams, categorically
The formalism Evan and I came up with for plate diagrams is to use doubly indexed categories of statistical theories. Given some schema for the hierarchy J, a theory can be a diagram in [|\mathsf{FinSet}|^J,C]. What does this look like? For a moment, let’s assume that J is the one object category for simplicity’s sake. Then we have the space of functors from |\mathsf{FinSet}| to C. There are a lot of these, but we are mainly concerned with \mathrm{const}_c, which sends I\mapsto c for all I, and s_c, which sends I\mapsto c^{\otimes I}. Using these, we can have access to all the unbiased powers of objects in C in the same place. Then, when J is nontrivial, our hierarchy can have different multiplicities in different parts. This allows us to create statistical theories for the hierarchical models described above, but more discussion on this topic is better saved for a future blog post.
3 Composing statistical theories
The real utility in separating syntax from semantics in statistical modelling is the ability to compare and combine statistical theories. Composition of statistical theories has been briefly described in (Patterson 2023), but I’d like to flesh out the idea a bit more here. By looking at the parameter and sample objects of a statistical theory as its domain and codomain, respectively, we can compose statistical theories by creating structured cospans from the inclusions of the (co)domains. Then theories can be composed in the manner of structured cospans, using pushouts. This is great, because in practice lots of statistical models are parameterized by the outputs of other statistical models. In fact, providing support for computing with and analyzing this sort of pattern is a large part of the motivation behind probabilistic programming languages.
4 What is a probabilistic programming language?
A probabilistic programming language is like a normal programming language but it has distributions as primitives and inference as a first class feature! In a normal PL, you can definitely do probabilistic programming, but the limited machinery for doing so causes things to get messy pretty quickly. Say you have a bunch of different branches based off samples from various distributions. You can then end up doing some thing. But it turns out, for a lot of applications it matters just as much how you get somewhere as where you end up. So maybe you modify your script to keep track of all the decisions you make. So now your program also outputs a list of samples along with its output. So then maybe you have some data corresponding to actual outputs of your program and you want to figure out what your samples should actually look like in order to expect to get that data. So you write some code that allows you to change the parameters, which did I mention you need to pass into your program every time?, in response to data in order to figure out what your program should actually be doing. See? Messy. And the way you end up having to do it in traditional programming languages just ends up feeling very backwards. Like, if we want to do these things they should be built into the way a function is defined, right? Thus, computer scientists created probabilistic programming languages, lands where sampling and inference rule.
5 Gen.jl
The land I have been sending our statistical theories to this summer is called Gen.jl (Cusumano-Towner et al. 2019). It has a bunch of cool features related to user specification of inference/sampling algorithms that I don’t really fully appreciate, but it’s well documented and has a simple enough syntax, which is what matters for our purposes.
In order to define a nondeterministic function in Gen, all you have to do is use the @gen macro and tell the compiler which variables to keep a trace of. In this situation, a trace is just a hashmap attaching random variables to their sampled values. Here is a simple example program from the Gen quickstart repo:
@gen function line_model(xs::Vector{Float64})
# We begin by sampling a slope and intercept for the line.
# Before we have seen the data, we don't know the values of
# these parameters, so we treat them as random choices. The
# distributions they are drawn from represent our prior beliefs
# about the parameters: in this case, that neither the slope nor the
# intercept will be more than a couple points away from 0.
slope = ({:slope} ~ normal(0, 1))
intercept = ({:intercept} ~ normal(0, 2))
# We define a function to compute y for a given x
function y(x)
return slope * x + intercept
end
# Given the slope and intercept, we can sample y coordinates
# for each of the x coordinates in our input vector.
for (i, x) in enumerate(xs)
# Note that we name each random choice in this loop
# slightly differently: the first time through,
# the name (:y, 1) will be used, then (:y, 2) for
# the second point, and so on.
({(:y, i)} ~ normal(y(x), 0.1))
end
# Most of the time, we don't care about the return
# value of a model, only the random choices it makes.
# It can sometimes be useful to return something
# meaningful, however; here, we return the function `y`.
return y
end;6 Statistical models as probabilistic programs
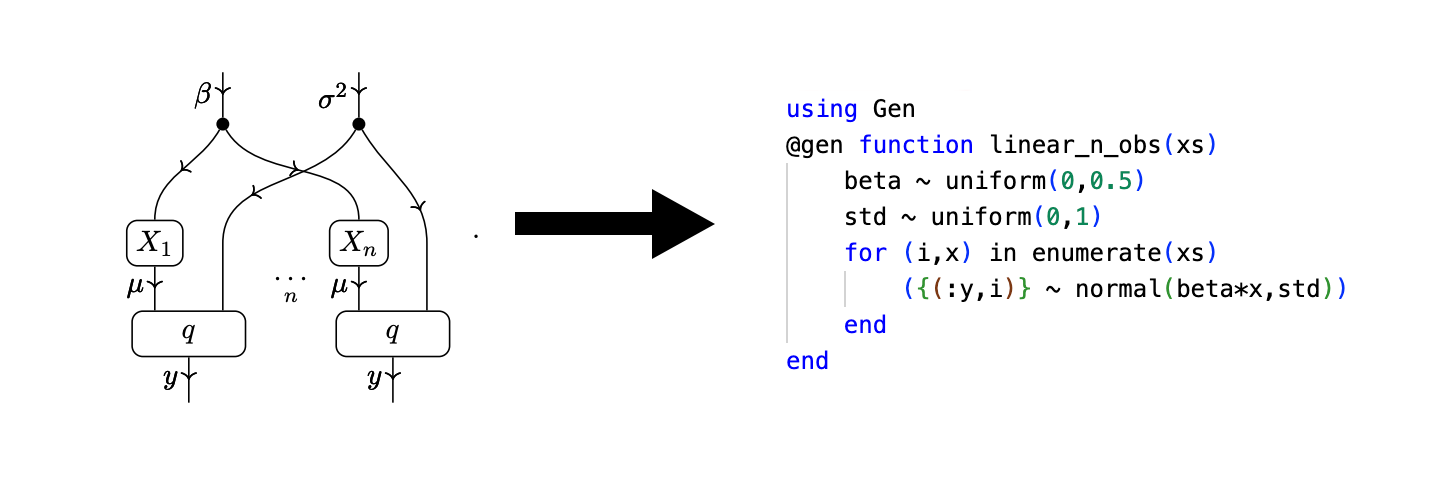
So we want to be able to do things with our categorically defined statistical models, right? Well then we’d better have a way to implement them in code! Rather than write our own PPL I decided to just use Gen. We can map morphisms to distributions and objects to samples from them to generate probabilistic programs from statistical models.
This is cool because if we want to do anything with our statistical models we need sampling/inference libraries, and implementing sampling algorithms is not necessarily how we want to spend our time. But if our model functor lands in PPL land, then we’ve struck gold! Some people really love to write sampling/inference algorithms and there’s tons of research & software around it. Honestly, we don’t need many of the feature Gen affords us for the current formalization of statistical models we use. Our statistical models don’t branch, which is kind of what PPLs are all about. But that’s for the next chapter. In this chapter I told you all about my proof-of-concept package for manipulating statistical theories and generating probabilistic programs which model them. Thanks for reading!